1、选择题  某人站在一台秤上，在他猛地下蹲的全过程中，台秤的读数?
A．先变大后变小，最后等于他的重力
B．变大，最后等于他的重力
C．先变小后变大，最后等于他的重力
D．变小，最后等于他的重力

参考答案：C

本题解析：下蹲的全过程包括向下的加速运动和向下的减速运动，向下的加速运动中加速度向下，重力大于支持力，读数变小。向下的减速运动中加速度向上，重力小于支持力，读数变大。最后静止，重力等于支持力。读数等于重力。答案选C。

本题难度：简单

2、选择题  如图所示，平行于光滑斜面的轻弹簧劲度系数为k，一端固定在倾角为的斜面底端，另一端与物块A连接，物块B沿斜面叠放在物块A上但不黏连。物块A、B质量均为m，初始时两物块均静止。现用平行于斜面向上的拉力F拉动物块B，使B做加速度为a的匀加速运动，两物块在开始一段时间内的v-t图象如图乙所示（t1时刻A、B的图线相切，t2时刻对应A图线的最高点），重力加速度为g，则?

A．A达到最大速度时的位移为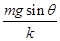
B．拉力F的 最小值为?
C．t1=时A、B分离
D．A、B分离前，A、B和弹簧系统机械能增加，A和弹簧系统机械能增加

参考答案：AC

本题解析：A中由图知，t2时刻A的加速度为零，速度最大，当AB静止时弹簧受到沿斜面方向向下的力，大小为2mgsinθ，当t2时刻时，A、B已经分离，A对弹簧的作用力是mgsinθ，故到的作用力变化了mgsinθ，根据胡克定律得：mgsinθ=kx，则A达到最大速度时的位移为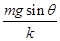，A是正确的；
B中对AB整体而言，根据牛顿第二定律得：F-2mgsinθ+kx=2ma，得F=2mgsinθ-kx+2ma，故x=0时，即开始时F最小，此时有：2mgsinθ=kx，得F的最小值为 F=2ma，故B不正确；
C中由图读出，t1时刻A、B开始分离，对A根据牛顿第二定律：kx-mgsinθ=ma，开始时有：2mgsinθ=kx0，又x0-x=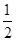at12，联立以上几个式子，解之得t1=，故C是正确的；
D中A、B分离前，F做正功，根据功能关系得知，A、B和弹簧系统机械能增加，而B对A的压力方向斜向下，做负功，故A和弹簧系统机械能减小，故D是不对的。

本题难度：一般

3、计算题  一只小猫跳起来抓住悬挂在天花板上的竖直木杆，如图所示，在这一瞬间悬绳断了，设木杆足够长，由于小猫继续上爬，所以小猫离地面高度不变，求木杆下降的加速度。（设小猫质量为m，木杆的质量为M）

参考答案：解：先对猫进行分析，由于猫相对地面高度不变，即猫处于平衡状态，而猫受重力G1=mg和木杆对猫向上的摩擦力F的作用，如图所示

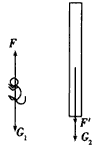
故G1与F二力平衡，即F=G1=mg ①
再对木杆进行受力分析：木杆受重力G2=Mg作用，由于木杆对猫有向上的摩擦力F，由牛顿第三定律可知，猫对杆有向下的摩擦力F"，且F"=F ②
由牛顿第二定律，杆的加速度为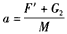?③
由①②③式可得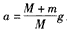
即杆下降的加速度为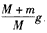，方向向下

本题解析：

本题难度：一般

4、简答题  如图所示，一块质量为M的木板沿倾斜角为θ的斜面无摩擦的下滑，现要使木板保持静止，则可知质量为m的人向下奔跑的加速度是多少？

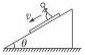
参考答案：对人和滑板整体受力分析，受重力、支持力，根据牛顿第二定律，有：
（M+m）gsinα=ma
解得a=(M+m)gsinθm
答：欲使木板静止在斜面上，木板上质量为m的人应以(M+m)gsinθm的加速度向下奔跑．

本题解析：

本题难度：一般

5、选择题  如图所示，轻弹簧上端与一质量为m的木块1相连，下端与另一质量为M的木块2相连，整个系统置于水平放置的光滑木板上，并处于静止状态。现将木板沿水平方向突然抽出，设抽出后的瞬间，木块1、2的加速度大小分别为a1、a2。重力加速度大小为g。则有

[? ]
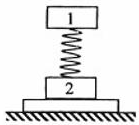
A．a1＝0
B．a1＝g
C．a2＝g
D．a2＝0

参考答案：AC

本题解析：

本题难度：一般