1、计算题  （13分）如图所示，在光滑的水平面上有一长为L的木板B，上表面粗糙，在其左端有一光滑的1/4圆弧槽C，与长木板接触但不相连，圆弧槽的下端与木板上表面相平，B、C静止在水平面上。现有滑块A以初速v0从右端滑上B，一段时间后，以v0/2滑离B，并恰好能到达C的最高点。A、B、C的质量均为m。求：

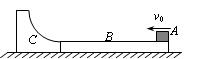
⑴A刚滑离木板B时，木板B的速度；
⑵A与B的上表面间的动摩擦因数μ；
⑶圆弧槽C的半径R；
⑷从开始滑上B到最后滑离C的过程中A损失的机械能。

参考答案：⑴v0/4 ⑵5v02/16gL （3）v02/64g（4）15mv02/32

本题解析：（1）对A在长木板B上的滑动过程，取ABC为一个系统，根据动量守恒定律有：
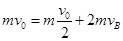解得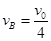
(2) 对A在长木板B上的滑动过程,ABC系统动能减少全部转化为系统的摩擦生热

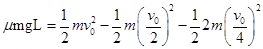
解得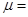5v02/16gL
⑶对A滑上C直到最高点的作用过程，AC系统动量守恒，mv0/2+mvB=2mv①
AC系统机械能守恒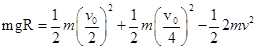?②
①②联立得R= v02/64g
⑷对A滑上C直到离开C的作用过程,AC系统动量守恒mv0/2+mv0/4=mvA+mvC①
AC系统初、末状态动能相等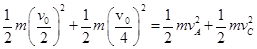，②
①②联立解得vA=v0/4。
所以从开始滑上B到最后滑离C的过程中A损失的机械能为：
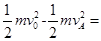15mv02/32

本题难度：一般

2、简答题  在水平光滑细杆上穿着A、B两个刚性小球（可看作质点），用两根长度同为L的不可伸长的轻绳与C球连接，如图所示．已知A、B、C三球质量均相同，开始时三球均静止、两绳伸直且处于水平状态．现同时释放三球，求：
（l）在C球运动到最低点．A、B两球刚要相碰的瞬间，A、B两球速度的大小；
（2）在A、B相碰前的某一时刻，A、B二球速度v的大小与C球到细杆的距离h之间的关系．

参考答案：

（1）C到达最低点时速度为零，设A、B、C的质量均为m，
A、C组成的系统在水平方向动量守恒，
由动量守恒定律得：mvA+mvB=0，
A、B、C组成的系统机械能守恒，
由机械能守恒定律可得：mgL=12mvA2+12mvB2，
解得：vA=

本题解析：

本题难度：一般

3、简答题  如图所示，长为L的木板A右边固定着一个挡板，包括挡板在内的总质量为1.5M，静止在光滑的水平地面上。有一质量为M的小木块B，从木板A的左端开始以初速度v0在
木板A上滑动。小木块B与木板A间摩擦因数为μ，小木块B滑到木板A的右端与挡板发生碰撞。已知碰撞过程时间极短，且碰后木块B恰好滑到木板A的左端就停止滑动。
（1）若μL=3v02/160g，在小木块B与挡板碰撞后的运动过程中，摩擦力对木板A做正功还是负功？做了多少？
（2）讨论木板A和小木块B在整个过程中，是否有可能在某一段时间内相对地面运动方向是向左的。如果不可能，说明理由；如果可能，求出至少可能向左滑动、又能保证木板A和小木块B刚好不脱离的条件。

参考答案：
（1）摩擦力对木板做负功，大小为（27/400）M v02
（2）B向左滑又不脱离A的条件是2v02/15g＜μL≤3v02/20g

本题解析：（1）设B与A碰撞后A、B的速度分别为vA、vB，最终A、B的共同速度为v，则由动量守恒、能量守恒有mBv0=mAvA+mBvB，mBv0=（mA+mB）v
μmBgL=（1/2）mAvA2+（1/2）mBvB2-（1/2）（mA+mB）v2
又μL=3v02/160g
以上各式联列解得v=（2/5）v0，vA=（1/2）v0，vB=（1/4）v0
或v=（2/5）v0，vA=（3/10）v0，vB=（11/20）v0
分析上述两组结果，由于两物碰撞后均与v0同向，而其中第二组结果vA=（3/10）v0＜vB=（11/20）v0，该速度关系与实际不符，舍去
因此，由动能定理可得摩擦力做功
Wf =（1/2）（1.5M）v2-（1/2）（1.5M）vA2=-（27/400）M v02
即摩擦力对木板做负功，大小为（27/400）M v02
（2）整个过程动量守恒，A不可能向左运动，碰后B可能。
要使B向左运动，由动量守恒、能量守恒有
mBv0=mAvA+mBvB，mBv0=（mA+mB）v
μmBgL=（1/2）mAvA2+（1/2）mBvB2-（1/2）（mA+mB）v2? vB＜0
以上各式联列解得μL＞2v02/15g
要保证A和B不脱离，由动量守恒和能量守恒有
mBv0=（mA+mB）v
2μmBgL≥（1/2）mBv02-（1/2）（mA+mB）v2
解得μL≤3v02/20g
故B向左滑又不脱离A的条件是2v02/15g＜μL≤3v02/20g

本题难度：一般

4、计算题  如图所示，质量m1=0.3kg 的小车静止在光滑的水平面上，车长L=15m，现有质量m2=0.2kg可视为质点的物块，以水平向右的速度v0=2m/s从左端滑上小车，最后在车面上某处与小车保持相对静止。物块与车面间的动摩擦因数μ=0.5，取g=10m/s2，求：物块在车面上滑行的时间t？

参考答案：解：设物块与小车的共同速度为v，以水平向右为正方向，根据动量守恒定律有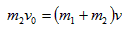①
设物块与车面间的滑动摩擦力为F，对物块应用动量定理有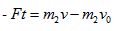
其中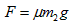②
解得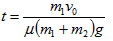，代入数据得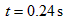③

本题解析：

本题难度：一般

5、计算题  （1） 氢原子第n能级的能量为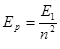，其中E1为基态能量。当氢原子由第4能级跃迁到基态时，发出光子的频率为v1；当氢原子由第2能级跃迁到基态时，发出光子的频率为v2，则=?。
（2）如图所示，质量M=4kg的滑板B静止放在光滑水平面上，其右端固定一根水平轻质弹簧，弹簧的自由端C互滑板左端的距离L=0.5m，这段滑板与木块A（可视为质点）之间的动摩擦因数，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑。小木块A以速度v0=10m/s由滑板B左端开始沿滑板的水平面上表面向右运动。已知木块A的质量m=1kg,g取10m/s2。求：

①弹簧被压缩到最短时木块A的速度；
②木块A压缩弹簧过程中弹簧弹势能最大值。

参考答案：（1）??（2）①?②

本题解析：（1）氢原子由第4能级跃迁到基态时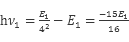，?； 氢原子由第2能级跃迁到基态时, ?， 所以
（2）①弹簧被压缩到最短时，木块A与滑板B具有相同的速度，设为，从木块A开始沿滑板B表面向右运动至弹簧被压缩到最短的过程中，A、B系统的动量守恒：
（2分）?
解得（1分）
代入数据得木块A的速度（2分）
②木块压缩弹簧过程中，弹簧被压缩到最短时，弹簧的弹性势能最大，由能量关系，弹簧的最大弹性势能为
（2分）
代入数据得（2分）

本题难度：一般