1、填空题  质量为2×103kg的汽车，发动机的最大输出功率为80kW，在平直的公路上受到4×103N的恒定阻力作用，则它能够达到的最大速度为______m/s；如果让汽车在公路上由静止开始以2m/s2的加速度做匀加速直线运动，则这个匀加速过程可以维持的时间为______s．

参考答案：当汽车以额定功率做匀速直线运动时，速度最大，则有F=F阻=4×103N
由P=Fvm，得? vm=PF=PF阻=800004×103m/s=20m/s．
?设汽车匀加速直线运动过程中牵引力为F1，根据牛顿第二定律得
? F1-F阻=ma，得到? F1=F阻+ma，
当汽车做匀加速直线运动功率达到额定功率时速度为
? v1=PF1=PF阻+ma
又v1=at得
? t=Pa(F阻+ma)
代入解得? t=5s
故答案为：20；5．

本题解析：

本题难度：一般

2、填空题  一只小猫跳起来抓住悬挂在天花板上的竖直木杆，如图所示，在这一瞬间悬绳断了，设木杆足够长，由于小猫继续向上爬，使得小猫离地面的高度不变，则木杆下落的加速度为____。（设小猫质量为m，木杆的质量为M）

参考答案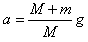：，方向竖直向下

本题解析：

本题难度：一般

3、计算题  分如图所示，质量为m=lkg的小物块由静止轻轻放在水平匀速运动的传送带上，从A点随传送带运动到水平部分的最右端B点，经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道，恰能做圆周运动。C点在B点的正上方，D点为轨道的最低点。小物块离开D点后，做平抛运动，恰好垂直于倾斜挡板打在挡板跟水平面相交的E点。已知半圆轨道的半径R=0．9 m，D点距水平面的高度h =0．75 m，取g="10" m/s2，

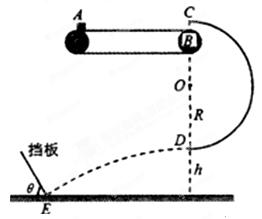
试求：
（1）摩擦力对物块做的功；
（2）小物块经过D点时对轨道压力的大小；
（3）倾斜挡板与水平面间的夹角θ。

参考答案：（1）摩擦力对物块做的功为4.5J；（2）小物块对轨道的压力大小为60N；倾斜挡板与水平面的夹角为θ为60°。

本题解析：
试题分析: 设小物块经过C点时的速度大小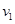,因为经过C时恰好能完成圆周运动，由牛顿第二定律可得：
；解得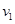=3m/s；
小物块由A到B过程中，设摩擦力对小物块做的功为W，由动能定理得：
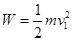，解得W=4.5J
故摩擦力对物块做的功为4.5J．
设小物块经过D点时的速度为，对由C点到D点的过程，由动能定理的：

小物块经过D点时，设轨道对它的支持力大小为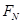，由牛顿第二定律得：

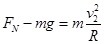
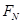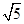联立解得=60N，=3m/s
由牛顿第三定律可知，小物块对轨道的压力大小为60N
小物块离开D点做平抛运动，设经时间t打在E点，由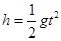
设小物块打在E点时速度的水平、竖直分量分别为，
=
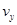
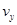=gt
又tanα==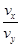
联立解得α=60°
再由几何关系可得θ=α=60°
故倾斜挡板与水平面的夹角为θ为60°．

本题难度：一般

4、选择题  如图所示，已知物体与三块材料不同的长方形板间的动摩擦因数分别为μ、2μ和3μ，三块板长度均为L，并排铺在水平地面上，该物体以一定的初速度v0从a点滑上第一块板，则物体恰好滑到第三块的末尾d点停下来，物体在运动中三块板均保持静止；若让物体从d点以相同大小的初速度水平向左运动，三块木板仍能保持静止，则下列说法正确的是（　　）

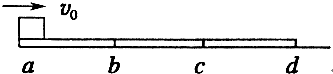
A．物体仍能运动到a点并停下来
B．物体不能运动到a点
C．物体两次经过c点时速度大小相等
D．物体两次经过b点时速度大小相等

参考答案：A、物块从a点开始向右运动过程，根据动能定理：μmgL+2μmgL+3μmgL=12mv02
假设物块从d向左运动过程能到达a点，则根据动能定理克服摩擦力做的功仍然为μmgL+2μmgL+3μmgL=12mv02
故物体仍嫩运动到a点停下来；故A正确B错误；
C、设速度大小相同的点为e点，e点在c点左侧s处
图示：
根据动能定理得：
向右运动过程：-μmgL-2μmg（L-s）=Eke-12mv02
向左运动过程：-3μmgL-2μmgS=Eke-12mv02由上两式得：
-3μmgL-2μmgS=-3μmgL+2μmgS
所以S=0，即为c点，故C正确D错误；
故选：AC．

本题解析：

本题难度：一般

5、简答题  在与x轴平行的匀强电场中，一带电量为2×10-6C、质量为4×10-2kg的带电物体在绝缘光滑水平面上沿着x轴做直线运动，其位移随时间的变化规律是x=0.3t-0.05t2，式中x、t均用国际单位制的基本单位．求：
（1）该匀强电场的场强；
（2）从开始运动到第5s末带电物体所运动的路程；
（3）若第6s末突然将匀强电场的方向变为+y轴方向，场强大小保持不变，在0～8s内带电物体电势能的增量．

参考答案：（1）根据位移与时间的关系式x=0.3t-0.05t2得知，带电体的初速度为v0=0.3m/s，加速度a=-0.1m/s2．
根据牛顿第二定律得：qE=ma，得场强E=Fq=maq
代入解得，E=2×103N/C?
（2）带电体速度减至零的时间为? t1=v0a=0.30.1s=3s?
则第3s末以后带电体沿相反方向做初速度为零的匀加速运动，时间t2=2s．
故第5s末带电物体所经过的路程为? s=x1+x2=（0.3t1-0.05t12）+12at22=（0.3×3-0.05×32）+12×0.1×22=0.65m?
（3）第1s末到第3s末带电体的位移大小为：x1=0.45m
第3s末到第6s末带电体的位移大小为：x3=12at23=0.45m
所以第6s末带电物体的位移为0，
第8s末位移为 y=12at22=120.1×22m=0.2m?
故带电物体电势能的增量为△E=-Eqy=-2×103×2×10-6×0.2J=-8×10-4J?
答：
（1）该匀强电场的场强是2×103N/C；
（2）从开始运动到第5s末带电物体所运动的路程是0.65m；
（3）若第6s末突然将匀强电场的方向变为+y轴方向，场强大小保持不变，在0～8s内带电物体电势能的增量是-8×10-4J．

本题解析：

本题难度：一般