|
高考物理试题《机械能综合应用》高频试题特训(2017年最新版)(二)
2017-08-05 16:48:11
来源:91考试网
作者:www.91exam.org 【 大 中 小】
|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 在一次探究活动中,某同学设计了如图所示的实验装置,将半径R="1" m的光滑半圆弧轨道固定在质量M="0.5" kg、长L="4" m的小车的上表面中点位置,半圆弧轨道下端与小车的上表面水平相切,现让位于轨道最低点的质量m="0.1" kg的光滑小球随同小车一起沿光滑水平面向右做匀速直线运动,某时刻小车碰到障碍物而瞬时处于静止状态(小车不反弹),之后小球离开圆弧轨道最高点并恰好落在小车的左端边沿处,该同学通过这次实验得到了如下结论,其中正确的是(g取10 m/s2) ( )

A.小球到达最高点的速度为 m/s m/s
B.小车与障碍物碰撞时损失的机械能为12.5 J
C.小车瞬时静止前、后,小球在轨道最低点对轨道的压力由1 N瞬时变为6.5 N
D.小车向右做匀速直线运动的速度约为6.5 m/s
|
参考答案:AB
本题解析:如图所示,

小球从B落到小车的左端边沿处所用时间t= = = s= s=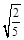 s。最高点的速度vB= s。最高点的速度vB=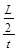 = = m/s= m/s= m/s,故A正确;小球从A到B只有重力做功,机械能守恒,有 m/s,故A正确;小球从A到B只有重力做功,机械能守恒,有 mvA2=mg2R+ mvA2=mg2R+ mvB2,代入数据解得vA= mvB2,代入数据解得vA=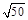 m/s≈7.1 m/s,这个速度等于小车匀速运动的速度,故D错误;小车与障碍物碰撞时损失的机械能E= m/s≈7.1 m/s,这个速度等于小车匀速运动的速度,故D错误;小车与障碍物碰撞时损失的机械能E= MvA2="12.5" J,B正确;小车瞬时静止前、后,小球在轨道最低点的速度不变,故对轨道的压力不变,C错误。 MvA2="12.5" J,B正确;小车瞬时静止前、后,小球在轨道最低点的速度不变,故对轨道的压力不变,C错误。
考点:机械能守恒定律、向心力、平抛运动
点评:本题把圆周运动、平抛运动巧妙地结合在一起,只要把受力分析弄精确,运动过程弄清楚,运动相应的知识就能求解。
本题难度:一般
2、其他
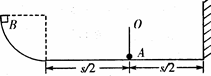
参考答案:12次
本题解析:

本题难度:一般
3、计算题 (9分)如图,质量m=1.0kg的物体(可视为质点)以v0=10m/s的初速度从水平面的某点向右运动并冲上半径R=1.0m的竖直光滑半圆环,物体与水平面间的动摩擦因数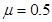 .求: .求:

(1)物体能从M点飞出,落到水平面时落点到N点的距离的最小值为多大?
(2)如果物体从某点出发后在半圆轨道运动过程途中离开轨道,求出发点到N点的距离x的取值范围.
参考答案:(1)2m;(2)8m>x>5m
本题解析:(1)物体恰好能从M点飞出,有: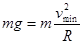 ① ①
由平抛运动知: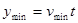 ② ②
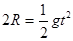 ③ (1分) ③ (1分)
解①②③得: 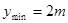 ④ ④
(2)(Ⅰ)物体不会在M到N点的中途离开半圆轨道,即物体恰好从M点飞出,物体从出发点到M过程.
由动能定理: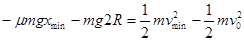 ⑤ ⑤
解①⑤得: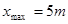 ⑥ ⑥
(Ⅱ)物体刚好至圆轨道圆心等高处速度为0,
由动能定理: 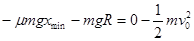 ⑦ ⑦
解⑦得: 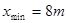 ⑧ ⑧
综上可得:8m>x>5m ⑨
考点:向心力、平抛运动、动能定理
本题难度:一般
4、计算题 (7分)为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接,如图所示。一个质量为2kg的小物块以初速度v0=4.0m/s,从某一高处水平抛出,恰从A点无碰撞地沿倾斜轨道滑下。已知物块与倾斜轨道AB的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8):
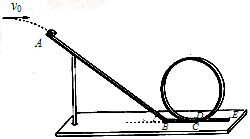
(1)求小物块的抛出点和A点的高度差;
(2)求小物块沿着轨道AB运动的过程中克服摩擦力所做的功;
(3)为了让小物块能沿着轨道运动,并从E点飞出,则竖直圆轨道的半径应该满足什么条件?
参考答案:(1)h=0.45m (2)W=16J (3)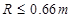
本题解析:(1)设从抛出点到A点的高度差为h,到A点时有则有:
 , ,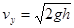 ,且 ,且  代入数据解得h="0.45m" (2分) 代入数据解得h="0.45m" (2分)
(2)小物块沿着轨道AB运动的过程中克服摩擦力所做的功
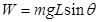
W=16J (2分)
(3)小物体到达A点时的速度: 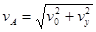 =5m/s (1分) =5m/s (1分)
从A到B,由动能定理:
小物体从B到环最高点机械能守恒: 
在最高点有: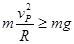 解得 解得 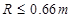 (2分) (2分)
考点:平抛运动、功、机械能守恒定律
本题难度:一般
5、选择题 如图所示,固定在水平面上的光滑斜面倾角为30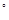 ,质量分别为M、m的两个物体通过细绳及轻弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M = 2m,空气阻力不计.松开手后,关于二者的运动下列说法中正确的是 ,质量分别为M、m的两个物体通过细绳及轻弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M = 2m,空气阻力不计.松开手后,关于二者的运动下列说法中正确的是

A.M和m组成的系统机械能守恒
B.当M的速度最大时,m与地面间的作用力为零
C.若M恰好能到达挡板处,则此时m的速度为零
D.若M恰好能到达挡板处,则此过程中重力对M做的功等于弹簧弹性势能的增加量与物体m的机械能增加量之和
|  ,此时m对地面的压力恰好为零,B正确;然后M做减速运动,当M恰好到达档板时,也就是速度刚好减小到了零,此时m受到的弹簧的弹力大于重力,还在加速上升,C错误;根据功能关系,M减小的机械能,等于m增加的机械能与弹簧增加弹性势能之和,而M恰好到达板时,动能恰好为零,因此减小的机械能等于减小的重力势能,即等于重力对M做的功,D正确。
,此时m对地面的压力恰好为零,B正确;然后M做减速运动,当M恰好到达档板时,也就是速度刚好减小到了零,此时m受到的弹簧的弹力大于重力,还在加速上升,C错误;根据功能关系,M减小的机械能,等于m增加的机械能与弹簧增加弹性势能之和,而M恰好到达板时,动能恰好为零,因此减小的机械能等于减小的重力势能,即等于重力对M做的功,D正确。