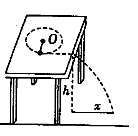
1、计算题  如图所示，一根长0.1m的细线，一端系着一个质量是0.18kg 的小球，拉住线的另一端，使球在光滑的水平桌面上做匀速圆周运动，当小球的转速增加到原转速的3倍时，细线断裂，这时测得断前瞬间线的拉力比原来大40N，求：
（1）线断裂的瞬间，线的拉力为多大；
（2）这时小球运动的线速度为多大；
（3）如果桌面高出地面0.8m，线断后小球飞出去落在离桌面的水平距离为多少的地方？（取10m/s2）

参考答案：解：（1）小球在光滑桌面上做匀速圆周运动时受三个力作用；重力mg、桌面弹力FN和细线的拉力F，
重力mg和弹力FN平衡，线的拉力提供向心力，，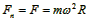
设原来的角速度为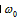，线上的拉力是，加快后的角速度为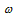，线断时的拉力是，
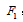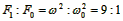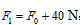则又，所以，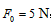
线断时。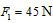
（2）设线断时小球的线速度大小为v，由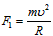，得。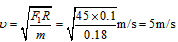
（3）由平抛运动规律得小球在空中运动的时间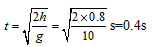
小球落地处离开桌面的水平距离。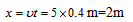

本题解析：

本题难度：困难

2、简答题  如图所示，在光滑水平面上有一光滑小孔O；一根轻绳穿过小孔，一端连接质量为m=1kg的小球A，另一端连接质量为M=4kg的重物B．（g=10m/s2）
（1）当小球A沿半径r=0.1m的圆周做匀速圆周运动，其角速度为ω=10rad/s，物体B对地面的压力为多大？
（2）当A球的角速度为多大时，B物体处于将要离开而尚未离开地面的临界状态？

参考答案：（1）设绳子上拉力为T，对根据向心力公式有：
T=mω2r=10N
对B根据平衡状态有：
Mg=T+FN
解得：FN=30N
由牛顿第三定律：FN′=FN=30N
故物体B对地面的压力为为30N．
（2）B物体处于将要离开而尚未离开地面的临界状态时地面给它的支持力为零，所以有：
绳子上拉力：T=Mg
对A根据向心力公式有：Mg=mω2r
解得：ω=20rad/s
当A球的角速度为20rad/s时，B物体处于将要离开而尚未离开地面的临界状态．

本题解析：

本题难度：一般

3、简答题  受控核聚变装置中有极高的温度，因而带电粒子将没有通常意义上的“容器”可装，而是由磁场约束带电粒子运动使之束缚在某个区域内．现按下面的简化条件来讨论这个问题：如图所示的是一个截面为内径R1=0.6m、外径R2=1.2m的环状区域，区域内有垂直于截面向里的匀强磁场．已知氦核的荷质比

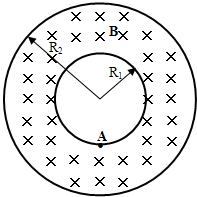
参考答案：

（l）根据质量数、电荷数守恒可知，氢核聚变反应的方程为：4?11H→?42He+2?01e+2v0?
质量亏损为：△m=4mp-mα-2me?
所以：△E=△mc2=（4mp-mα-2me）c2?
（2）设氦核质量为m，电量为q，以速率v在磁感强度为B的匀强磁场中做半径为r的匀速圆周运动，
由洛仑兹力公式和牛顿定律得：
Bqv=mv2r?
解得：v=Bqrm
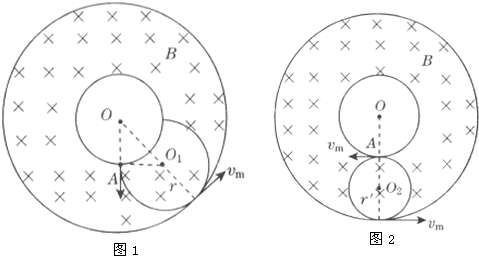
（3）所求轨迹示意图如图1所示（要与外圆相切）?
（4）当氦核以vm的速度沿与内圆相切方向射入磁场且轨道与外圆相切时，则以vm速度沿各方向射人磁场区的氦核都不能穿出磁场外边界，如图2所示，由图可知：r′=R2-R12
由①式可得：r=mvBq
在速度为vm时不穿越磁场外界应满足的条件是：mvmBq≤r′
代入数据可得：vm≤5.76×104m/s
答：（1）氢核聚变反应的方程为：4?11H→?42He+2?01e+2v0，一次核反应所释放能量的表达式为（4mp-mα-2me）c2；
（2）v与r的关系式为v=Bqrm；
（3）如图所示；
（4）氦核的最大速度为5.76×104m/s；

本题解析：

本题难度：一般

4、简答题  如图所示．细绳长L，吊一个质量为m的铁球，细绳到大小为2mg的拉力会断裂，绳的上端系一质量不计的环，环套在光滑水平杆上，起初环带着球一起以v=

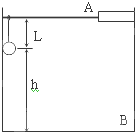
参考答案：环被A挡住的瞬间有：
T-mg=mv2r
解得：T=2mg
故绳断
若先碰地，则有：2L=12gt2解得：t=

本题解析：

本题难度：一般

5、简答题  某段铁路转弯处的圆弧半径为r，两铁轨高度差为h，两铁轨间距离为L，火车转弯时可以简化为质点做圆周运动，问：
（1）当列车的运动速率为多大时，车轮才恰好与铁轨间不发生侧压．
（2）若列车通过转弯处速度过快，可能产生怎样后果？（不必分析理由）
（3）随着人们生活节奏加快，对交通运输的快捷提出了更高的要求，国家对铁路运输不断进行提速，如果要求列车通过铁路转弯处速率也相应提高，且车轮与铁轨间仍不发生侧压，在原来铁路转弯处应进行怎样的改造？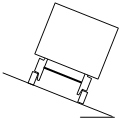

参考答案：

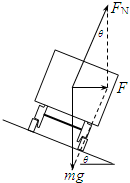
（1）列车受力如图所示，根据牛顿第二定律得
mgtanθ=mv2r?
由几何关系得?tanθ=h

本题解析：

本题难度：一般