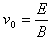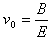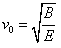1、计算题  (19分)如图甲所示，竖直挡板MN左侧空间有方向竖直向上的匀强电场和垂直纸面向里的水平匀强磁场，电场和磁场的范围足够大，电场强度E=40N/C，磁感应强度B随时间t变化的关系图象如图乙所示，选定磁场垂直纸面向里为正方向。t=0时刻，一质量m=8×10-4kg、电荷量q=+2×10-4C的微粒在O点具有竖直向下的速度v=0.12m/s，O?是挡板MN上一点，直线OO?与挡板MN垂直，取g=10m/s2。求：
（1）微粒再次经过直线OO?时与O点的距离；
（2）微粒在运动过程中离开直线OO?的最大高度；
（3）水平移动挡板，使微粒能垂直射到挡板上，挡板与O点间的距离应满足的条件。

参考答案：（1）1.2m
（2）2.48m
（3）L=（2.4n+1.8) m （n=0，1，2…)

本题解析：（1）由题意可知，微粒所受的重力G=mg=8×10-3N
电场力大小F=Eq=8×10-3N
因此重力与电场力平衡 ,微粒先在洛伦兹力作用下做匀速圆周运动（3分）
?解得?R =="0.6m?" （2分）
由??解得T="10πs?" （2分）
则微粒在5πs内转过半个圆周，再次经直线OO?时与O点的距离l=2R ="1.2m?" （2分）
（2）微粒运动半周后向上匀速运动，运动的时间为t=5πs，轨迹如图所示，

位移大小?s=vt="0.6πm=1.88m?" ?（3分）
因此，微粒离开直线OO?的最大高度
h=s+R="2.48m?" （3分）
（3）若微粒能垂直射到挡板上的某点P，P点在直线OO?下方时，由图象可知，挡板MN与O点间的距离应满足
L=（2.4n+0.6)m（n=0，1，2…)?（2分）
若微粒能垂直射到挡板上的某点P，P点在直线OO?上方时，由图象可知，挡板MN与O点间的距离应满足
L=（2.4n+1.8) m （n=0，1，2…)?（2分）
［若两式合写成L=（1.2n+0.6) m （n=0，1，2…)同样给4分］

本题难度：一般

2、计算题  PQ为一根足够长的绝缘细直杆，处于竖直的平面内，与水平夹角为q斜放，空间充满磁感应强度B的匀强磁场，方向水平如图所示。一个质量为m，带有负电荷的小球套在PQ杆上，小球可沿杆滑动，球与杆之间的摩擦系数为（），小球带电量为q。现将小球由静止开始释放，试求小球在沿杆下滑过程中：

（1）小球最大加速度为多少？此时小球的速度是多少？
（2）下滑过程中，小球可达到的最大速度为多大？

参考答案：（1），?（2）

本题解析： （1）当小球所受的洛伦兹力小于重力垂直杆向下的分力，小球向下做加速运动，洛伦兹力逐渐增大，支持力和滑动摩擦力逐渐减小，合力增大，加速度增大．当洛伦兹力大于重力垂直杆的分力时，杆对小球的支持力方向变为垂直于杆向下，速度增大，滑动摩擦力增大，合力减小，加速度减小，则当洛伦兹力等于于重力垂直杆向下的分力时，支持力和摩擦力为零，合力最大，加速度最大，根据牛顿第二定律得：
，得到最大加速度为
由得，?
（2）当洛伦兹力大于重力垂直杆的分力时，小球做匀速直线运动时，速度最大，由平衡条件得：

解得，最大速度为
点评：注意本题中小球受到的洛伦兹力是变化的，所以杆对小球的支持力大小和方向也是变化的。

本题难度：一般

3、选择题  如图所示为一速度选择器，两极板P、Q之间距离为d，且P接电源负极，Q接正极；板内有一磁感应强度为B，方向垂直纸面向外的匀强磁场，一束粒子流以速度v流经磁场时恰好不偏转（不计重力），则两极板必须加上一定电压U；则下列说法中正确的是（　　）
A．U=Bvd，粒子一定带正电
B．U=Bv，粒子一定带负电
C．U=Bvd，粒子一定从a运动到b
D．U=Bvd，粒子可能从b运动到a