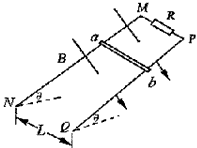
1、计算题  如图所示，两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上，两导轨间距为L0，M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上，并与导轨垂直。整套装置处于磁感应强度为B的匀强磁场中，磁场方向垂直斜面向下，导轨和金属杆的电阻可忽略。让ab杆沿导轨由静止开始下滑，导轨和金属杆接触良好，不计它们之间的摩擦。
（1）由b向a方向看到的装置如图所示，请在此图中画出ab杆下滑过程中某时刻的受力示意图；
（2）在加速下滑过程中，当ab杆的速度大小为v时，求此时ab杆中的电流及其加速度的大小；
（3）求在下滑过程中，ab杆可以达到的速度最大值。

参考答案：（1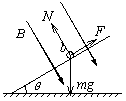）（2），
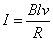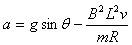
（3）

本题解析：

本题难度：困难

2、选择题  如图是法拉第做成的世界上第一台发电机模型的原理图。将铜盘放在磁场中，让磁感线垂直穿过铜盘；a、b导线与铜盘的中轴线处在同一竖直平面内；转动铜盘，可以使闭合电路获得电流。若图中铜盘半径为L，匀强磁场的磁感应强度为B，回路总电阻为R，从上往下看逆时针匀速转动铜盘的角速度为ω。则下列说法正确的是

[? ]
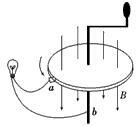
A．回路中有大小和方向周期性变化的电流
B．回路中电流大小恒定，且等于
C．回路中电流方向不变，从b导线流进灯泡，再从a导线流向旋转的铜盘
D．若将匀强磁场改为仍然垂直穿过铜盘的正弦变化的磁场，不转动铜盘，灯泡中也会有电流流过

参考答案：C

本题解析：

本题难度：一般

3、计算题  如图所示（俯视），MN和PQ是两根固定在同一水平面上的足够长且电阻不计的平行金属导轨．两导轨间距为L=0.2m，其间有一个方向垂直水平面竖直向下的匀强磁场B1=5.0T。导轨上NQ之间接一电阻R1=0.40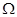，阻值为R2=0.10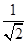的金属杆垂直导轨放置并与导轨始终保持良好接触。两导轨右端通过金属导线分别与电容器C的两极相连。电容器C紧靠着带小孔a（只能容一个粒子通过）的固定绝缘弹性圆筒。圆筒内壁光滑，筒内有垂直水平面竖直向下的匀强磁场B2，O是圆筒的圆心，圆筒的内半径为r=0.40m。

（1）用一个大小恒为10N，平行于MN水平向左的外力F拉金属杆，使杆从静止开始向左运动求：当金属杆最终匀速运动时杆的速度大小；
（2）当金属杆处于（1）问中的匀速运动状态时，电容器C内紧靠极板且正对a孔的D处有一个带正电的粒子从静止开始经电容器C加速后从a孔垂直磁场B2并正对着圆心O进入筒中，该带电粒子与圆筒壁碰撞四次后恰好又从小孔a射出圆筒。已知粒子的比荷q/m=5×107（C/kg），该带电粒子每次与筒壁发生碰撞时电量和能量都不损失，不计粒子重力和空气阻力，则磁感应强度B2多大（结果允许含有三角函数式）。

参考答案：（1）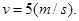
（2）（ⅰ）情形1：每段轨迹圆弧对应的圆心角为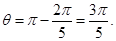
得：?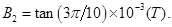
（ⅱ）情形2：每段轨迹圆弧对应的圆心角为?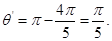
将数据代式得?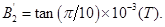

本题解析：（1）金属杆先做加速度变小的加速运动，最终以最大速度匀速运动.设杆匀速运动时速度为v，



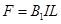
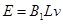
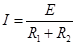
将已知数据代入得：?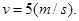
（2）设杆匀速运动时C两极板间的电压为U，带电粒子进入圆筒的速率为V.在磁场中作匀速圆周运动的半径为R，由于C与电阻R1并联，
据欧姆定律得，?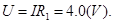
据动能定理有，?
带电粒子在磁场中作匀速圆周运动，?
由于带电粒子与圆筒壁碰撞时无电量和能量损失，那么每次碰撞前后粒子速度大小不变.速度方向总是沿着圆筒半径方向，4个碰撞点与小孔a恰好将圆筒壁五等分，粒子在圆筒内的轨迹具有对称性，由5段相同的圆弧组成，设每段轨迹圆弧对应的圆心角为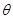，则由几何关系可得：?
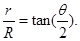有两种情形符合题意（如图所示）：

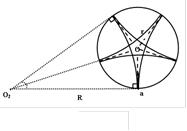
（ⅰ）情形1：每段轨迹圆弧对应的圆心角为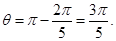
得：?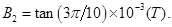
（ⅱ）情形2：每段轨迹圆弧对应的圆心角为?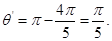
将数据代式得?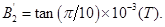

本题难度：一般

4、选择题  如图所示，在电容器C的两端接有一个圆环形导体回路，在圆环回路所围的面积之内存在着垂直纸面向里的匀强磁场B，已知圆环的半径r=5cm，电容器的电容C=20F，当磁场B以2×10－2T／s的变化率均匀增加时，则电容器的

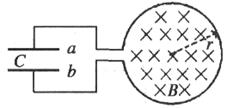
A．a板带正电，电荷量为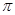×10－9C
B．a板带负电，电荷量为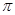－×10－9C
C．a板带正电，电荷量为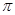×10－6C
D．a板带负电，电荷量为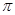－×10－6C

参考答案：A

本题解析：由法拉第电磁感应定律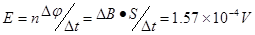，由Q=CU可知电荷量为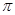×10－9C，由楞次定律可判断电源正负极，注意在电源内部电流由负极流向正极，A对；

本题难度：简单

5、计算题  如图14所示，两条足够长的平行长直金属细导轨KL、PQ固定于同一水平面内，它们之间的距离为L，电阻可忽略不计，ab和cd是两根质量皆为m的金属细杆，杆与导轨垂直，且与导轨良好接触，并可沿导轨无摩擦地滑动。两杆的电阻皆为R，杆cd的中点系一轻绳，绳的另一端绕过轻的定滑轮悬挂一质量为M的物体，滑轮与转轴之间的摩擦不计，滑轮与杆cd之间的轻绳处于水平伸直状态并与导轨平行．导轨和金属细杆都处于匀强磁场中，磁场方向垂直于导轨所在平面向上，磁感应强度的大小为B。现两杆及悬挂物都从静止开始运动．求：
(1)当ab杆及cd杆的速度分别达到v1和v2时，两杆加速度的大小各为多少？
(2)最终ab杆及cd杆的速度差为多少(两杆仍在导轨上运动)?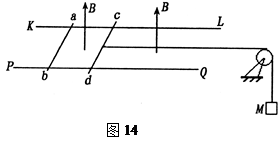

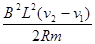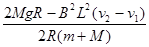参考答案：（1）a1=? a2=（2）

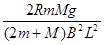
本题解析：本题考查双轨道切割磁感线的问题，两条导体棒切割磁感线产生的感应电动势方向相反， 回路中的电动势为E1=BL(v2－v1) ，再由牛顿第二定律求出加速度
(1)用E1和I1分别表示abdc回路的感应电动势和感应电流的大小，根据法拉第电磁感应定律和欧姆定律可知
E1=BL(v2－v1)? ………………………2分
I1=E1/2R? ……………………1分
令F1表示磁场对每根杆的安培力的大小，则F1=I1BL? ……………1分
令a1和a2分别表示ab杆、cd杆和物体M加速度的大小，F2表示绳中张力的大小，由牛顿定律可知
F1= ma1? ……………………………………………2分
Mg－F2=Ma2? ……………………………………………2分
F2－F1=ma2? ……………………………………………2分
由以上各式解得?
a1=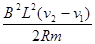? ……………………………………………1分
a2=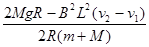? ……………………………………………1分
(2)最终ab杆及cd杆的加速度相同，设其为a，速度差为?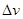
E2=BL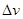? I2=E/2R……………………………2分
令F3表示磁场对每根杆的安培力的大小，则F3=I2BL……………………………………………1分
F4表示绳中张力的大小，由牛顿定律可知
F3= ma? ……………………………………………1分
Mg－F4=Ma? ……………………………………………1分
F4－F3=ma? ……………………………………………1分
由以上各式解得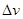=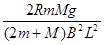? ……………………………2分

本题难度：一般