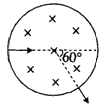
1、填空题  如图所示，圆形区域内有垂直于纸面向里的匀强磁场，磁感应强度为B，一带电粒子（不计重力）以某一初速度沿圆的直径方向射入磁场，粒子穿过此区域的时间为t，粒子飞出此区域时的速度方向偏转角为60°，根据上述条件可求出下列物理量中的____。
①带电粒子的比荷
②带电粒子的初速度
③带电粒子在磁场中运动的周期
④带电粒子在磁场中运动的半径

参考答案：①③

本题解析：

本题难度：一般

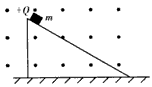
2、选择题  如图所示，表面粗糙的斜面固定于地面上，并处于方向垂直纸面向外、磁感应强度为B的匀强磁场中。质量为m、带电荷量为+Q的小滑块从斜面顶端由静止下滑，在滑块下滑的过程中。下列判断正确的是

[? ]
A．滑块受到的摩擦力不变
B．滑块到地面时的动能与B的大小无关
C．滑块受到的洛伦兹力方向垂直斜面向下
D．B很大时，滑块可能静止于斜面上

参考答案：CD

本题解析：

本题难度：一般

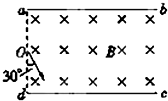
3、简答题  一足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场，矩形区域的左边界ad长为L，现从ad中点O垂直于磁场射入一速度方向与ad边夹角为30°、大小为v0的带正电粒子，如图所示．已知粒子电荷量为q，质量为m（重力不计）：
（1）若要求粒子能从ab边射出磁场，v0应满足什么条件？
（2）若要求粒子在磁场中运动的时间最长，粒子应从哪一条边界处射出？最长时间是多少？出射点位于该边界上何处？

参考答案：（1）粒子带正电，粒子运动的轨迹如图所示，当粒子的速度大于与R1相对应的速度v1时，粒子将恰好不从dc边射出．
由几何关系可得：R1=L…①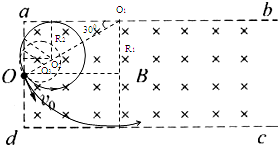
由洛仑兹力和向心力公式可得：qv1B=mv12R1…②
当粒子的速度小于与R2相对应的速度v2时，粒子将从ad边射出．
由几何关系可得：R2+R2sin30°=12L…③
由③式解得：R2=13L…④
由洛仑兹力和向心力公式可得：qv2B=mv22R2…⑤
将①④式分别代入②⑤式可解得v1=qBLm，v2=qBL3m
所以v0的取值范围是qBL3m＜v0≤qBLm．
（2）若粒子在磁场中运动的时间最长，其对应的圆周运动的圆心角必然最大，在答图中，当粒子的速度小于v2时，粒子从ad边的不同位置射出时，其半径虽不同，但圆心角的夹角都是56×2π，所以粒子在磁场中的运动时间也是56T，此即粒子在磁场中运动的最长时间．
粒子运动的周期：T=2πRv=2πmqB所以粒子运动的最长时间为：t=56T=5πm3qB
.OP= 2R2sin30°=R2=13L
即：粒子将从O点上方的13L的范围射出磁场．
答：（1）若要求粒子能从ab边射出磁场，v0应满足qBL3m＜v0≤qBLm．
（2）若要求粒子在磁场中运动的时间最长，粒子应从ad边界处射出，最长时间是5πm3qB，
出射点位于该边界上O点上方13L处．

本题解析：

本题难度：一般

4、简答题  如图所示，在平行于纸面的平面上建立一个xoy平面直角坐标系，在此坐标系的第一象限内有垂直纸面向里的匀强磁场，磁感应强度为B．一个反质子（质量与质子相同，电荷与质子等值反性）和一个．粒子从坐标原点0垂直磁场方向以相同速度v进入磁场中，速度方向与x轴夹角为30°．已知，反质子的质量为m，带电量为e且为负电荷，a粒子的质量为4m，带电量为2e．
（1）反质子和a粒子在磁场中运动时间之比是多少？
（2）分别求出这两个粒子射出磁场区时的位置坐标．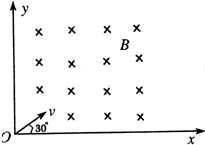

参考答案：（1）依题知粒子在磁场中受洛伦兹力作用而做匀速圆周运动，设圆周运动半径为R，周期为T，由牛顿第二定律得


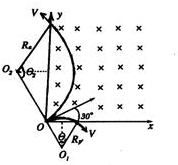
? qvB=mmv2R
则得 R=mvqB，T=2πRv=2πmqB
反质子的轨道半径为RP′=mveB，周期为TP′=2πmeB
α粒子的轨道半径为 Rα=4mv2eB=2mveB
Tα=2π?4m2eB=4πmeB
它们的运动轨迹如图所示，由几何知识知，反质子运动的轨迹对应的圆心角为θ1=60°=π3
α粒子运动的轨迹对应的圆心角为θ2=120°=2π3
则反质子在磁场中运动的时间为 tP′=16TP′=16×2πmeB=mπ3eB
α粒子在磁场中运动的时间为tα=13Tα=4πm3eB
∴反质子和α粒子在磁场中运动时间之比是tP′tα=14
（2）反质子和α粒子这两个粒子射出磁场区时的横坐标和纵坐标分别为xP′和yα．
根据几何知识得
? xP′=2RP′sin30°? yα=2Rα=2

本题解析：

本题难度：一般

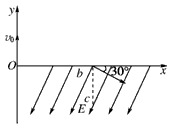
5、计算题  如图所示，一质量为m、电荷量为＋q的粒子，以速度v0从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域，磁场方向垂直纸面向外，粒子飞出磁场区域后，从b处穿过x轴进入场强为E、方向与x轴负方向成60°角斜向下的匀强电场中，速度方向与x轴正方向的夹角为30°，经过一段时间后恰好通过b点正下方的c点，粒子的重力不计。试求：
(1)圆形匀强磁场的最小面积；
(2)c点到b点的距离d。

参考答案：解：(1)粒子在磁场中做匀速圆周运动，由qBv0＝m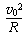，得R＝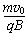
粒子经过磁场区域速度偏转角为120°，这表明在磁场区域中运动轨迹为半径为R的圆弧，作出粒子运动轨迹如图中实线所示。所求圆形磁场区域的最小半径为


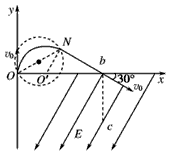
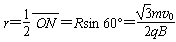
面积为S＝πr2＝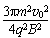
(2)粒子进入电场做类平抛运动，从b到c垂直电场方向位移为x′＝v0t ①
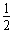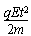沿电场方向位移为y′＝at2＝?②
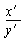＝tan30° ③
解方程①②③得x′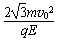＝，y′＝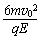
d＝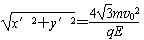

本题解析：

本题难度：困难