1、单选题  定义4△5=4+5+6+7+8=30，7△4=7+8+9+10=34，按此规律，(26△15)+(10△3)的值为_____。
A: 528
B: 525
C: 423
D: 420
参考答案: A
本题解释:正确答案是A考点计算问题解析三角符号代表着以符号前一个数为首项，符号后的数为项数，公差为1的一个等差数列，用等差公式求和，26△15=26+…+40=(26+40)×15÷2=495，10△3=10+11+12=33，因此和值为528。故答案为A。

2、单选题  甲某打电话时忘记了对方电话号码最后一位数字，但记得这个数字不是"0"。甲某尝试用其他数字代替最后一位数字，恰好第二次尝试成功的概率是_____。
A: 1/9
B: 1/8
C: 1/7
D: 2/9
参考答案: A
本题解释:正确答案是A考点概率问题解析最后一个数字不是0，共有9种选择。要求恰好第二次尝试成功，则第一次尝试失败，概率为8/9，第二次更换数字成功，概率为1/8，因此恰好第二次尝试成功的概率为8/9×1/8=1/9。故正确答案为A。秒杀技根据不放回摸球模型，恰好第二次尝试成功的概率与恰好第一次成功的概率相同，因此该概率值为1/9。故正确答案为A。

3、单选题  在空间中最多能放置多少个正方体，使得任意两个正方体都有一部分表面相接触?_____
A: 4
B: 5
C: 6
D: 7
参考答案: A
本题解释:正确答案是A考点几何问题解析注意到一个立方体的六个面，形成3组相对面，而一组相对面上不可能同时贴有立方体，因此一个立方体周围最多可以贴3个立方体，故最多能放置4个立方体，使得任意两个立方体均有部分表面相接触。下图即为一个示例：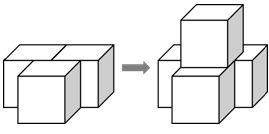

4、单选题  甲公司的一分厂制造了10台机床，二分厂制造了8台。乙公司向甲公司购买6台机床，丙公司向甲公司购买12台机床。每台机床的运费因运输距离的不同而有差异，具体情况如下表所示。乙、丙两公司购买机床的运费总和最低为_____元。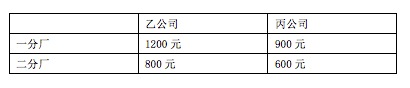A: 12000
B: 13500
C: 15000
D: 16000
参考答案: C
本题解释:正确答案是C考点统筹规划问题解析乙、丙公司从一分厂购买机床的价格分别为1200、900元，乙、丙公司从二分厂购买机床的价格分别为800、600元，乙、丙公司在一、二分厂的购买价格相差400、300元，为了使乙、丙两个公司的运费最低，二分厂的的机床都应该运至乙公司，乙丙最低运费为：6×800+2×600+(12-2)×900=4800+1200+9000=15000(乙公司买二分厂的6台机床，丙公司购买二分厂过剩余的2台机床和一分厂的10台机床)，故购买机床的最低运费为15000元。故正确答案为C。

5、单选题  工人甲一分钟可生产螺丝3个或螺丝帽9个，工人乙一分钟可生产螺丝2个或螺丝帽7个，现在两人各花20分钟，共生产螺丝和螺丝帽134个，问生产的螺丝比螺丝帽多几个?_____
A: 34个
B: 32个
C: 30个
D: 28个
参考答案: A
本题解释:正确答案是A考点不定方程问题解析设两人20分钟全部生产螺丝，则共生产了100个，注意到甲生产螺帽比螺丝每分钟多6个，乙每分钟多5个。设甲生产螺帽X分钟，乙生产螺帽Y分钟，根据鸡兔同笼原理，有6X+2Y=134-100，当X=4，Y=2时，符合条件，再代入计算，得螺帽有4×9+2×7=50个，螺丝有84个，则螺丝比螺帽多84-50=34个。故正确答案为A。