1、单选题 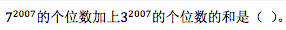 A: 5
B: 8
C: 10
D: 13
参考答案: C
本题解释:正确答案是C考点计算问题解析

2、单选题  现有甲、乙两个水平相当的技术工人需进行三次技术比赛，规定三局两胜者为胜方。如果在第一次比赛中甲获胜，这时乙最终取胜的可能性有多大?_____。
A: 1/3
B: 1/4
C: 1/2
D: 1/6
参考答案: B
本题解释:正确答案是B考点概率问题解析比赛为三局两胜制，甲先赢一场，故乙赢得比赛，下两场必须都胜利。而甲乙水平相当，故每场赢得比赛的概率都为0.5，则乙最后赢得比赛的概率为0.5×0.5=0.25，即1/4，故正确答案为B。

3、单选题  甲乙两人计划从A地步行去B地，乙早上7：00出发，匀速步行前往，甲因事耽搁，9：00才出发。为了追上乙，甲决定跑步前进，跑步的速度是乙步行速度的2.5倍，但每跑半小时都需要休息半小时，那么甲什么时候才能追上乙?_____
A: 10：20
B: 12：10
C: 14：30
D: 16：10
参考答案: C
本题解释:正确答案是C考点行程问题解析解析1：设乙步行速度为1，则甲跑步速度为2.5，则9:00时甲乙两人之间的距离为2，5小时后，两人相距2-(2.5×0.5-1)×5=0.75，此时，再经过半小时甲刚好追上乙，即共用了5个半小时，在14:30追上，故正确答案为C。解析2：

4、单选题  甲乙两人从相距1350米的地方，以相同的速度相对行走，两人在出发点分别放下1个标志物。再前进10米后放下3个标志物。前进10米放下5个标志物，再前进10米放下7个标志物，以此类推。当两个相遇时，一共放下了几个标志物?_____
A: 4489
B: 4624
C: 8978
D: 9248
参考答案: D
本题解释:正确答案是D考点数列问题解析以10米为间隔，可知1350米的路程被分成135个间隔，因此共有136个放标志物的点，按甲乙平分为两组，每组为68个点，故甲或乙最后均放置135个标志物。由求和公式可知总数为(1+135)÷2×68×2=9248。因此正确答案为D。注：等差数列求和公式，和=(首项+末项)×项数÷2秒杀技易知全程被分为135个间隔，从而得出每组放置标志物的点为偶数，注意到每次放下标志物都为奇数，从而可知每组的标志物总数必然为偶数。又考虑到甲乙两组是相同的，而选项中C、D分别为A、B的两倍，而A、B中B为偶数，故可猜测B为一人放下的标志物数，而D为答案。标签猜题技巧

5、单选题  科考队员在冰面上钻孔获取样本，测量不同空心之间的距离，获得的部分数据分别为1米、3米、6米、12米、24米、48米。问科考队员至少钻了多少个孔?_____
A: 4
B: 5
C: 6
D: 7
参考答案: D
本题解释:正确答案是D考点几何问题解析所测距离组成一个数列1、3、6、12、24、48，易知该数列中任一项均大于其前面所有项之和，故这6条线段不可能组成封闭回路，即6条线段最少7个端点，至少钻7个孔。故正确答案为D。