1、单选题  某市一条大街长7200米，从起点到终点共设有9个车站，那么每个车站之间的平均距离是_____。
A: 780米
B: 800米
C: 850米
D: 900米
参考答案: D
本题解释:正确答案是D考点计数模型问题解析该问题为计数模型中的植树问题。车站间的平均距离为7200÷(9-1)=900。故正确答案为D。

2、单选题  用两根同样长度的铁丝分别圈成圆形和正方形，圆形面积大约是正方形面积的几倍?_____
A: 3/π
B: 4/π
C: 5/π
D: 6/π
参考答案: B
本题解释:正确答案是B考点几何问题解析设圆的半径为r，则正方形的面积为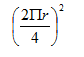

3、单选题  一艘游轮逆流而行，从A地到B地需6天；顺流而行，从B地到A地需4天。问若不考虑其他因素，一块塑料漂浮物从B地漂流到A地需要多少天？_____
A: 12天
B: 16天
C: 18天
D: 24天
参考答案: D
本题解释:正确答案是D解析设两地距离为12，则逆流速度＝12÷6＝2，顺流速度＝12÷4＝3，顺流速度－水流速度＝逆流速度＋水流速度，则水流速度＝0.5，所以漂流时间＝12÷0.5＝24天，故正确答案为D。行程问题标签顺水漂流模型赋值思想

4、单选题  四年级有4个班，不算甲班其余三个班的总人数是131人;不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人，问这四个班共有多少人?_____
A: 177
B: 178
C: 264
D: 265
参考答案: A
本题解释:正确答案是A考点和差倍比问题解析解析1：设甲、乙、丙和丁四个班的人数分别为a、b、c和d，根据题意可得，b+c+d=131，a+b+c=134，b+c-(a+d)=-1，联立解得：a+d=89，b+c=88，因此四个班总人数为：89+88=177，故选择A选项。解析2：因为乙、丙两班总人数比甲、乙两班总人数少1人，因此乙、丙两班总人数的3倍就等于(131+134-1)即为264人，乙、丙两班共有：264÷3=88(人)，因此四个班总人数为：88+88+1=177，故选择A选项。秒杀技由“乙、丙两班总人数比甲、乙两班总人数少1人”可知四个班总人数一定为奇数，观察到只有A和D选项符合，而通过题意可知四个班总人数一定小于：131+134=265，故只有A选项符合。标签直接代入数字特性

5、单选题  一个金鱼缸，现已注满水。有大、中、小三个假山，第一次把小假山沉入水中，第二次把小假山取出，把中假山沉入水中，第三次把中假山取出，把小假山和大假山一起沉入水中。现知道每次从金鱼缸中溢出水量的情况是：第一次是第二次的1/3，第三次是第二次的2倍。问三个假山的体积之比是多少?_____
A: 1：3：5
B: 1：4：9
C: 3：6：7
D: 6：7：8
参考答案: B
本题解释:正确答案是B考点和差倍比问题解析放入小假山，溢出水的体积为V，则小假山的体积为V;小假山取出，放入中假山，中假山除了将已溢出的体积V填满，还溢出3V体积的水，则中假山的体积是4V;同理，小假山和大假山除了将已溢出的体积4V填满，还溢出了6V，则大假山的体积为4V+6V-V=9V，可得三者之比为1：4：9。故正确答案为B。