1、单选题  有颜色不同的五盏灯，每次使用一盏、两盏、三盏、四盏和五盏，并按一定次序挂在灯杆上表示不同的信号，这些颜色不同的灯共可以表示多少种不同的信号?_____
A: 240
B: 300
C: 320
D: 325
参考答案: D
本题解释:正确答案是D考点排列组合问题解析

2、单选题  木工师傅为下图所示的3层模具刷漆，每层模具分别由1、3、6个边长1米的正方形组成。如果用一公斤漆可以刷20平方米的面积。那么为这个3层模具的所有外表面上色，需要几公斤漆?_____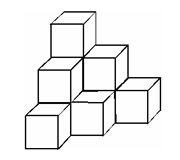A: 1.8
B: 1.6
C: 1.5
D: 1.2
参考答案: A
本题解释:正确答案是A考点几何问题解析堆积模具两个侧面及底面各有1+2+3个正方形，而斜坡方向上有这样组合3个，因此左右模具共有表面积为6×6=36平方米。因此需要油漆1.8公斤。因此正确答案为A。

3、单选题  科考队员在冰面上钻孔获取样本，测量不同空心之间的距离，获得的部分数据分别为1米、3米、6米、12米、24米、48米。问科考队员至少钻了多少个孔?_____
A: 4
B: 5
C: 6
D: 7
参考答案: D
本题解释:正确答案是D考点几何问题解析所测距离组成一个数列1、3、6、12、24、48，易知该数列中任一项均大于其前面所有项之和，故这6条线段不可能组成封闭回路，即6条线段最少7个端点，至少钻7个孔。故正确答案为D。

4、单选题  连接正方体每个面的中心构成一个正八面体(如下图所示)。己知正方体的边长为6厘米，问正八面体的体积为多少立方厘米?_____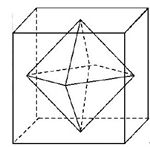A: 182
B: 242
C: 36
D: 72
参考答案: C
本题解释:正确答案是C考点几何问题解析正八面体可以拆解成两个完全相同的四棱锥，每个棱锥的体积V=1/3Sh，高度h为正方体边长的一半，h=3厘米，棱锥的底面是下面正方体横截面(从正中切开)里的小正方形，因此棱锥的底面积是正方体底面积的一半：6×6÷2=18平方厘米，每个棱锥的体积为1/3×18×3=18立方厘米，该正八面体的体积为18×2=36立方厘米，故正确答案为C。

5、单选题  分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9
B: 17/35
C: 101/203
D: 151/301
参考答案: D
本题解释:正确答案是D考点其他解析4/9、17/35、101/203、3/7、151/301中只有151/301大于1/2，其他数字均小于1/2，因此151/301最大，故正确答案为D。