1、单选题  甲容器中有浓度为4％的盐水250克，乙容器中有某种浓度的盐水若干克。现从乙中取出750克盐水，放人甲容器中混合成浓度为8%的盐水。问乙容器中的盐水浓度约是多少？_____
A: 9.78%
B: 10.14%
C: 9.33%
D: 11.27%
参考答案: C
本题解释:正确答案是C解析浓度问题标签十字交叉法

2、单选题  某天，林伯的水果摊三种水果的价格分别为：苹果6元/斤，芒果5元/斤，香蕉3/斤。当天，苹果与芒果的销售量之比为4：3，芒果与香蕉的销售量之比为2：11，卖香蕉比卖苹果多收入102元，林伯这天共销售三种水果_____斤。
A: 75
B: 94
C: 141
D: 165
参考答案: B
本题解释:正确答案是B考点经济利润问题解析将两个比例合并：苹果与芒果的销售量之比为8：6，芒果与香蕉的销售量之比为6：33。故苹果、芒果、香蕉的销售量之比为8：6：33。故设三者的销售量分别为8x、6x、33x，从而有3×33x-6×8x=102，解得x=2。故共销售水果(8+6+33)×2=94斤。故正确答案为B。

3、单选题  甲乙两人计划从A地步行去B地，乙早上7：00出发，匀速步行前往，甲因事耽搁，9：00才出发。为了追上乙，甲决定跑步前进，跑步的速度是乙步行速度的2.5倍，但每跑半小时都需要休息半小时，那么甲什么时候才能追上乙?_____
A: 10：20
B: 12：10
C: 14：30
D: 16：10
参考答案: C
本题解释:正确答案是C考点行程问题解析解析1：设乙步行速度为1，则甲跑步速度为2.5，则9:00时甲乙两人之间的距离为2，5小时后，两人相距2-(2.5×0.5-1)×5=0.75，此时，再经过半小时甲刚好追上乙，即共用了5个半小时，在14:30追上，故正确答案为C。解析2：

4、单选题  一项工程由甲、乙、丙三个工程队共同完成需要15天，甲队与乙队的工作效率相同，丙队3天的工作量与乙队4天的工作量相同，三队同时开工2天后，丙队被调往另一工地，甲、乙两队留下继续工作。那么，开工22天以后，这项工程_____。
A: 已经完工
B: 余下的量需甲乙两队共同工作1天
C: 余下的量需乙丙两队共同工作1天
D: 余下的量需甲乙丙三队共同工作1天
参考答案: D
本题解释:正确答案是D考点工程问题解析设工程总量为150，则甲、乙、丙三个工程队每天效率的和为150÷15=10，又知"甲队与乙队的工作效率相同，丙队3天的工作量与乙队4天的工作量相同"，可知甲、乙和丙三个工程队每天效率分别为3、3和4，开工22天，即甲和乙工作22天，丙工作2天，此时剩余工程量为：150-(3+3)×22-4×2=10，因此余下工作量需甲乙丙三队共同工作1天即可，故正确答案为D。标签赋值思想

5、单选题  如右图所示，△ABC是等腰直角三角形，AB=12，AD的长度是CD的2倍，四边形EBCD与△AED的面积之比为3：2，AE的长度是_____。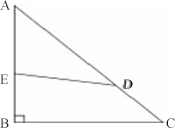A: 6.9
B: 7.1
C: 7.2
D: 7.4
参考答案: C
本题解释:正确答案是C考点几何问题解析四边形EBCD与三角形AED的面积之比为3：2，则三角形ABC与三角形AED的面积之比为5：2。已知AD的长度是CD的2倍，则AD的长度是AC的2/3。作DF垂直AB于点F，则DF=2/3BC(相似三角形原理)，三角形ABC的面积=1/2×AB×BC，三角形AED的面积=1/2×AE×DF=1/2×AE×2/3BC代入之前的比例式，可得AE=3/5AB=36/5=7.2。所以正确答案为C。