1、单选题  甲有桌子若干张，乙有椅子若干把。如果乙用全部椅子换回数量同样多的桌子，则需补给甲320元;如果乙不补钱，就要少换回5张桌子。已知3张桌子比5把椅子的价钱少48元，那么乙原有椅子多少把?_____
A: 16
B: 20
C: 48
D: 56
参考答案: B
本题解释:正确答案是B考点和差倍比问题解析由“如果乙用全部椅子换回数量同样多的桌子，则需补给甲320元;如果乙不补钱，就要少换回5张桌子”，可知每张桌子的价钱为：320÷5=64，又知“已知3张桌子比5把椅子的价钱少48元”，可知椅子的价钱为：(64×3+48)÷5=48，那么每张桌子比椅子贵：64-48=16，又知“如果乙用全部椅子换回数量同样多的桌子，则需补给甲320元”，即相同数量的桌子和椅子总的差价为320元，则乙原有的椅子数量为：320÷16=20，故选择B选项。

2、单选题  一公司销售部有4名区域销售经理，每人负责的区域数相同，每个区域都正好有两名销售经理负责，而任意两名销售经理负责的区域只有1个相同。问这4名销售经理总共负责多少个区域的业务?_____
A: 12
B: 8
C: 6
D: 4
参考答案: C
本题解释:正确答案是C考点容斥原理问题解析由题意，每个区域正好有两名销售经理负责，可知2个经理一组对应一个区域;而根据，任意两名销售经理负责的区域只有1个相同，可知2个经理一组仅对应一个区域。由此两条可知，区域数其相当于从4个经理中任选2个有多少种组合，一种组合就对应一个区域，故共有6个区域。因此正确答案为C。

3、单选题  _____ A: A
B: B
C: C
D: D
参考答案: B
本题解释:正确答案是B考点几何问题解析因为正三角形的周长和正六边形的周长相等，又因为正三角形和正六边形的边长的个数比是1：2，所以其边长之比为2：1，假设正三角形的边长为2，则正六边形的边长为1。正六边形可以分成6个小正三角形，如下图所示，边长为1的小正三角形面积：加长为2的正三角形面积=1：4。所以正六边形面积：正三角形面积=6：4=1.5，故正确答案为B。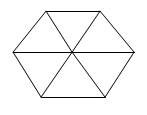

4、单选题  甲、乙、丙、丁四人做手工纸盒，已知甲、乙、丙三人平均每人做了28个，乙、丙、丁三人平均每人做了31个，已知丁做了33个，问甲做了多少个?_____
A: 24个
B: 26个
C: 27个
D: 28个
参考答案: A
本题解释:正确答案是A考点平均数问题解析由题意，甲、乙、丙共做了28×3=84个，乙、丙、丁共做了31×3=93个，则丁比甲多做了93-84=9(个)，已知丁做了33个，那么甲做了33-9=24个，故正确答案为A。

5、单选题  将25台笔记本电脑奖励给不同的单位，每个单位奖励的电脑数量均不等，最多可以奖励几个单位?_____
A: 5
B: 6
C: 7
D: 8
参考答案: B
本题解释:正确答案是B考点数列问题解析解析1：从1台开始算起，1+2+3+4+5+6=21，还多4台，不能再单独奖励给一个单位，只能分到后4个单位，因此最多可以奖励6个单位，故正确答案为B。