1、单选题  有一列数：3，7，10，17，27，44…从第三个数起，每个数都等于它前面两个数的和，那么第1998个数除以5的余数是多少?_____
A: 4
B: 3
C: 2
D: o
参考答案: D
本题解释:参考答案
题目详解:我们将这列数每个数分别被5除，观察余数有什么规律。这列数每个数分别被5除所得的余数依次是：3，2，0，2，2，4，1，0，1，1，2，3，0，3，3，1，4，0，4，4，3，2，0，2，2，4，1，0，…从上述结果可知，余数每20个数出现一周期循环。那么有：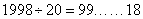

2、单选题  从装满1000克浓度为50%的酒精瓶中倒出200克酒精，再倒入蒸馏水将瓶加满。这样反复三次后，瓶中的酒精浓度是多少_____
A: 22.5%
B: 24.4%
C: 25.6%
D: 27.5%
参考答案: C
本题解释:【解析】C。每次操作后，酒精浓度变为原来的，因此反复三次后浓度变为。

3、单选题  某代表团有756名成员，现要对A、B两议案分别进行表决，且他们只能投赞成票或反对票。已知赞成A议案的有476人，赞成B议案的有294人，对A、B两议案都反对的有169人，则赞成A议案且反对B议案的有_____。
A: 293人
B: 297人
C: 302人
D: 306人
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析解析1：反对B议案的有756-294=462人，两者都反对的共169人，则赞成A且反对B的有462-169=293人。故正确答案为A。解析2：赞成A或B议案的人有756-169=587人，赞成A议案的有476人，赞成B议案的有294人，则两者都赞成的共476+294-587=183人，则赞成A且反对B的有476-183=293人。故正确答案为A。标签两集合容斥原理公式公式应用

4、单选题  筑路队原计划每天筑路720米，实际每天比原计划多筑路80米，这样在规定完成全路修筑任务的前3天，就只剩下1160米未筑，这条路全长多少千米?_____
A: 8.10
B: 10.12
C: 11.16
D: 13.50
参考答案: C
本题解释:C解析：现在每天筑路：720+80=800（米）规定时间内，多筑的路是：（720+80）×3-1160=2400-1160=1240（米）求出规定的时间是1240÷80=15.5（天），这条路的全长是,720×15.5=11160（米）。故本题选C。

5、单选题  三位专家为10幅作品投票，每位专家分别都投出了5票，并且每幅作品都有专家投票。如果三位专家都投票的作品列为A等，两位专家投票的列为B等，仅有一位专家投票的作品列为C等，则下列说法正确的是_____。
A: A等和B等共6幅
B: B等和C等共7幅
C: A等最多有5幅
D: A等比C等少5幅
参考答案: D
本题解释:【答案】D。解析：解析1：分别以等级代表其数量，根据题意可得A＋B＋C＝10……①；3A＋2B＋C＝15……②②－①×2可得：C－A＝5，因此正确答案为D。解析2：代入选项法。根据题意可得A＋B＋C＝10……①；3A＋2B＋C＝15……②此时有3个未知量，只有2个方程，典型的不定方程问题。将选项代入，依次验证是否成立即可。以选项A为例，若选项A正确，则有：A＋B＝6。到此得到第三个方程，便可求解此方程组，得C＝4，A＝－1，B＝7。故排除A。类似的方法可排除选项B、C。故正确答案为D。解析3：根据题意可得A＋B＋C＝10……①；3A＋2B＋C＝15……②由②－①消去C，可得2A＋B＝5。由于A、B、C均为非负整数，由此可知0≤2A≤5，因此A只能取值0、1、2。依次代回，可得A、B、C的可能取值为0、5、5；1、3、6；2、1、7三种情形，只有选项D上述三组数据都符合。故正确答案为D。解析4：根据题意可得A＋B＋C＝10……①；3A＋2B＋C＝15……②对不定方程而言，往往不能得到唯一的一组解。但从选项容易看出，只要求出其中一组解即可验证不符合的选项，将其排除掉即可。因此令A＝0，发现B＝5、C＝5，符合非负整数要求。此时可迅速排除前两个选项，而选项C显然错误。故正确答案为D。