1、单选题  先将线段AB分成20等份，线段上的等分点用”△”标注，再将该线段分成21等份，等分点用”O”标注(A、B两点都不标注)，现在发现”△”和”O”之间的最短处长为2厘米，问线段AB的长度为多少?_____
A: 2460厘米
B: 1050厘米
C: 840厘米
D: 680厘米
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析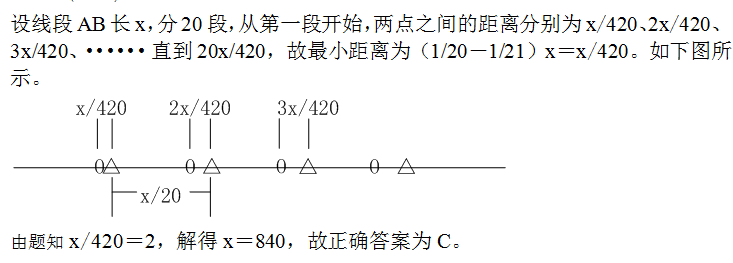

2、单选题  某班有60名学生，在第一次测验中有32人得满分，在第二次测验中有27人得满分。如果两次测验中都没有得满分的学生有17人，那么两次测验中都获得满分的人数是多少?_____
A: 13人
B: 14人
C: 15人
D: 16人
参考答案: D
本题解释:正确答案是D考点容斥原理问题解析本题注意按照得满分得到两个类，进行容斥原理分析。设第一次测验得满分为事件A，第二次测验得满分为事件B，则两次都得满分为A∩B，将其设为x人，得过满分为A∪B。根据公式A∪B=A+B-A∩B可得：60-17=32+27-x解得x=16，因此两次测验中都获得满分的人数是16人，故正确答案为D。

3、单选题  某医院内科病房有护士15人，每两人一班，轮流值班，每8小时换班一次，某两人同值一班后，到下次这两人再同值班，最长需要几天_____
A: 15 
B: 35 
C: 30 
D: 5
参考答案: B
本题解释:B.【解析】n×（n-1）/2=15×14/2=105，105×8/24=35。故选B。

4、单选题  A、B两数恰含有质因数3和5，它们的最大公约数是75，已知A数有12个约数，B数有10个约数，那么，A、B两数的和等于_____。
A: 2500
B: 3115
C: 2225
D: 2550
参考答案: D
本题解释:参考答案
题目详解:由题目可知，A、B两数之和是75的倍数，选项中只有D是75的倍数。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数

5、单选题  甲、乙、丙、丁四人共做零件325个。如果甲多做10个，乙少做5个，丙做的个数乘以2，丁做的个数除以3，那么，四个人做的零件数恰好相等。问：丁做了多少个?_____
A: 180
B: 158
C: 175
D: 164
参考答案: A
本题解释:正确答案是A考点和差倍比问题解析假设相等的个数为x，则甲做的个数为x-10，乙为x+5，丙为x/2，丁为3x，根据题意可得(x-10)+(x+5)+x/2+3x=325，解得x=60。则丁做的个数为60×3=180(个)，因此答案为A。秒杀技由题意，丁的个数可以被3整除，排除B、C、D，故正确答案为A。