1、单选题  100人参加7项活动，已知每个人只参加一项活动，而且每项活动参加的人数都不一样，那么，参加人数第四多的活动最多有几个人参加?_____
A: 22
B: 21
C: 24
D: 23
参考答案: A
本题解释:总的人数是固定的100人，要使参加人数第四多的活动最多，且每项的人数不一样，则其他的项的人数要尽量的少，那么，最后三名人数最少分别为1，2，3。设第四名的人数为x人，则前三名最少分别为（x+1），（x+2），（x+3），那么：1+2+3+x+（x+1）+（x+2）+（x+3）=100，解得x=22，故参加人数第四多的活动最多有22人参加。故选A。

2、单选题  计算：(1×2×3+2×4×6+…+100×200×300)/(2×3×4+4×6×8+…+200×300×400)的值为_____。
A: 1/8 
B: 1/4 
C: 3/2 
D: 5/4
参考答案: B
本题解释:B【解析】分析分子部分每个加数(连乘积)的因数，可以发现前后之间的倍数关系，从而把“1×2×3”作为公因数提到前面，分母部分也做类似的变形。原式=1×2×3+8×(1×2×3)+…+1000000×(1×2×3)2×3×4+8×(2×3×4)+…+1000000×(2×3×4)=[1×2×3×(1+8+…+1000000)]/[2×3×4×(1+8+…+1000000)]=(1×2×3)/(2×3×4)=1/4因此，本题正确答案为B。

3、单选题  某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训? _____
A: 8 
B: 10 
C: 12 
D: 15
参考答案: D
本题解释:【解析】D。本题可直接看出答案，乙教室一次45人，共有1290人，所以乙次数一定为偶数，又因为一共27次，所以甲一定为奇数，直接选15。

4、单选题  某商店有126箱苹果，每箱至少有120个苹果，至多有144个苹果。现将苹果个数相同的箱子算作一类。设其中箱子数最多的一类有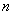A: 4
B: 5
C: 6
D: 7
参考答案: C
本题解释:参考答案:C
题目详解:解法一：将苹果个数相同的箱子算成一类，那么每一类都可以看成一个“抽屉”。这样可以构造出144-120+1=25个抽屉，又由于：126÷25=5…1，由抽屉原理2可以得到，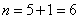

5、单选题  423×187-423×24-423×63的值是_____。
A: 41877 
B: 42300 
C: 42323 
D: 42703
参考答案: B
本题解释: B 【解析】原式可化为423×（187-24-63）。