1、单选题  某单位有60名运动员参加运动会开幕式，他们着装白色或黑色上衣，黑色或蓝色裤子。其中有12人穿白上衣蓝裤子，有34人穿黑裤子，29人穿黑上衣，那么穿黑上衣黑裤子的有多少人?_____
A: 12
B: 14
C: 15
D: 19
参考答案: C
本题解释:正确答案是C考点容斥原理问题解析解析1：穿白色上衣的有60-29=31人，其中穿白上衣黑裤子的有31-12=19人，穿黑上衣黑裤子的有34-19=15人。解析2：设白上衣黑裤子有a人，黑上衣黑子裤有b人，黑上衣蓝裤子有c人，根据题意有a+b+c=60-12，a+b=34，b+c=29，则b=34+29-(60-12)=15人。故正确答案为C。

2、单选题  甲班与乙班同学同时从学校出发去某公园，甲班步行的速度是每小时4千米，乙班步行的速度是每小时3千米。学校有一辆汽车，它的速度是每小时48千米，这辆汽车恰好能坐一个班的学生。为了使这两班学生在最短的时间内到达，那么，甲班学生与乙班学生需要步行的距离之比是_____。
A: 15：11
B: 17：22
C: 19：24
D: 21：27
参考答案: A
本题解释:正确答案是A考点和差倍比问题解析设甲步行X小时，乙步行Y小时。故可得方程4X+48Y=3Y+48X，解得X：Y=45：44，所以步行距离之比4X：3Y=15：11，故正确答案为A。

3、单选题  _____ A: A
B: B
C: C
D: D
参考答案: B
本题解释:正确答案是B考点几何问题解析因为正三角形的周长和正六边形的周长相等，又因为正三角形和正六边形的边长的个数比是1：2，所以其边长之比为2：1，假设正三角形的边长为2，则正六边形的边长为1。正六边形可以分成6个小正三角形，如下图所示，边长为1的小正三角形面积：加长为2的正三角形面积=1：4。所以正六边形面积：正三角形面积=6：4=1.5，故正确答案为B。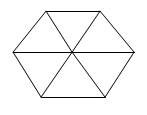

4、单选题  如右图所示，△ABC是等腰直角三角形，AB=12，AD的长度是CD的2倍，四边形EBCD与△AED的面积之比为3：2，AE的长度是_____。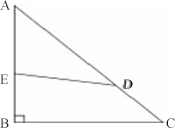A: 6.9
B: 7.1
C: 7.2
D: 7.4
参考答案: C
本题解释:正确答案是C考点几何问题解析四边形EBCD与三角形AED的面积之比为3：2，则三角形ABC与三角形AED的面积之比为5：2。已知AD的长度是CD的2倍，则AD的长度是AC的2/3。作DF垂直AB于点F，则DF=2/3BC(相似三角形原理)，三角形ABC的面积=1/2×AB×BC，三角形AED的面积=1/2×AE×DF=1/2×AE×2/3BC代入之前的比例式，可得AE=3/5AB=36/5=7.2。所以正确答案为C。

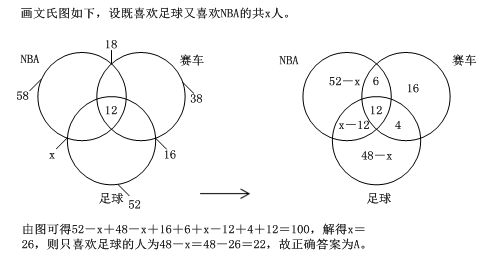
5、单选题  对厦门大学计算机系100名学生进行调查，结果发现他们喜欢看NBA和足球、赛车。其中58人喜欢看NBA;38人喜欢看赛车，52人喜欢看足球，既喜欢看NBA又喜欢看赛车的有18人，既喜欢看足球又喜欢看赛车的有16人，三种都喜欢看的有12人，则只喜欢看足球的有_____。
A: 22人
B: 28人
C: 30人
D: 36人
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析