1、单选题  现有21朵鲜花分给5人，若每个人分得的鲜花数各不相同，则分得鲜花最多的人至少分得_____朵鲜花。
A: 7
B: 8
C: 9
D: 10
参考答案: A
本题解释:正确答案是A考点多位数问题解析要使分得最多花的人分到的花尽可能的少，那么其他人分到的花尽可能的多。5人分到的花应尽量接近，以保证分得最多花的人分到的花尽可能少，所以最好是5个连续的自然数，21÷5=4.2，所以5人先分花数为2、3、4、5、6。2+3+4+5+6=20，还剩1朵花未分出。剩下的1朵花只能分给之前分到6朵花的人。则分得最多的人至少分得7朵鲜花，正确答案为A。

2、单选题  A: A
B: B
C: C
D: D
参考答案: D
本题解释:正确答案是D考点计算问题解析解析1：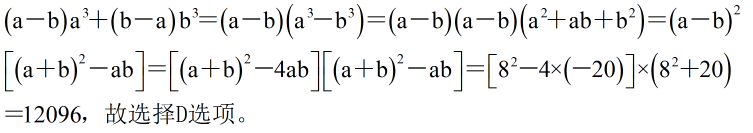

3、单选题  完成某项工程，甲单独工作需要18小时，乙需要24小时，丙需要30小时。现按甲、乙、丙的顺序轮班工作，每人工作一小时换班。当工程完工时，乙总共干了多少小时?_____
A: 8小时
B: 7小时44分
C: 7小时
D: 6小时48分
参考答案: B
本题解释:正确答案是B考点工程问题解析解析1：设工程总量为360，则甲乙丙的工作效率分别为20、15、12，三人每小时工作总量为47。由题意可知三人轮班即为循环周期问题，用360除以47商7余数为31，甲乙丙轮班每人7小时后，乙继续工作的工作量为31-20=11。所以最终乙总共干了：7小时+11/15×60分=7小时44分，故正确答案为B。解析2：设工程总量为360，则甲乙丙的工作效率分别为20、15、12，甲每小时比乙多干5，乙每小时比丙多干3，因此乙工作时间必定小于24/3=8小时。观察选项有6小时、7小时和8小时，可选7为参考点，甲乙丙轮班每人工作7小时共完成：(20+15+12)×7=329<360，因此乙工作时间在7小时和8小时之间，故正确答案为B。

4、单选题  甲、乙、丙三辆车的时速分别为60公里、50公里和40公里，甲从A地，乙和丙从B地同时出发相向而行，途中甲遇到乙后15分钟又遇到丙，问A、B两地相距多少公里?_____
A: 150公里
B: 250公里
C: 275公里
D: 325公里
参考答案: C
本题解释:正确答案是C考点行程问题解析解析1：甲乙相遇时，甲走了全程的60÷(50+60)=6/11;甲丙相遇时，甲走了全程的60÷(40+60)=6/10;在甲乙相遇之后到甲丙相遇，甲走了全程的6/10-6/11=3/55，这段路程为60×15/60=15(公里)，所以AB相距15÷(3/55)=275(公里)。解析2：设AB相距s公里，则s/(60+50)=s/(60+40)-1/4，解得s=275(公里)。故正确答案为C。

5、单选题  “红星”啤酒开展”7个空瓶换1瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期间共喝掉347瓶”红星”啤酒，问张先生最少用钱买了多少瓶啤酒?_____
A: 296瓶
B: 298瓶
C: 300瓶
D: 302瓶
参考答案: B
本题解释:正确答案是B考点计数模型问题解析7个空瓶换1瓶啤酒可表示为：7空瓶=1空瓶+1啤酒，可推知：6空瓶=1啤酒，假设最少要买x瓶，则有：x+[x/6]=347，将各选项代入知选项B中的298使得上述方程成立，故选择B选项。备注：此处的[x/6]表示取x/6的整数部分。标签直接代入