1、单选题  一个自然数被6除余4，被8除余6，被10除余8，那么这个数最小为多少?_____
A: 58
B: 66
C: 118
D: 126
参考答案: C
本题解释:参考答案:C
题目详解:此题为剩余定理中差同的情况。根据"差同减差，最小公倍数做周期"可知：这个自然数加上2以后，就能够被6、8和10整除;而6、8和10的最小公倍数是120：因此，这个数最小为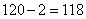

2、单选题  有一段阶梯，如果每步跨4级，最后会剩下2级，如果每步跨5级，最后则会剩下1级。已知这段阶梯的级数可以被3整除，则这段阶梯共有_____级。
A: 42
B: 46
C: 63
D: 66
参考答案: D
本题解释:参考答案:D
题目详解:设阶梯共有

3、单选题  一个自然数，被7除余2，被8除余3，被9除余1，1000以内一共有多少个这样的自然数?_____
A: 5
B: 2
C: 3
D: 4
参考答案: B
本题解释:参考答案:B
题目详解:7、8的最小公倍数为56，根据"差同减差，公倍数做周期"可知：所有满足条件的数可表示为56n-5，也就是除以56余5;要让所有56n-5中满足被9除余1：最小数是n=3时：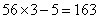

4、单选题  有一筐苹果，把它们三等分后还剩2个苹果;取出其中两份，将它们三等分后还剩两个：然后再取出其中两份，又将这两份三等分后还剩2个。问：这筐苹果至少有几个_____
A: 19
B: 23
C: 24
D: 26
参考答案: B
本题解释:参考答案:B
题目详解:根据中国剩余定理：我们面对着最后剩下的2个苹果，它们是把某两份苹果三等分后剩下的;换句话说，把所剩的2个苹果与三等分的三份苹果放在一起，应是上一轮分割中的两份;所以这个总数必须能被2整除。题中又问这筐苹果"至少"有几个：从而上述总数又应尽可能地少，三份苹果中，每份最少有1个苹果，于是三份便是3个。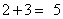

5、单选题  一个数除以5余4，除以8余3，除以11余2，求满足条件的最小的自然数是多少?_____
A: 19
B: 99
C: 199
D: 299
参考答案: D
本题解释:参考答案:D
题目详解:此题采用层层推进法：一个数除以5余4：那么用4加上5的倍数，直至除以8余3为止;可以得到