1、单选题  一个边长为1的正方形木板，锯掉四个角使其变成正八边形，那么正八边形的边长是多少?_____ A: A
B: B
C: C
D: D
参考答案: D
本题解释:正确答案是D考点几何问题解析

2、单选题  一条双向铁路上有11个车站，相邻两站都相距7千米。从早晨7点，有18列货车由第11站顺次发出，每隔5分钟发一列，都驶向第一站，速度都是每小时60千米;早晨8点，由第1站发一列客车，向第11站驶出，时速100千米，在到达终点前，货车与客车都不停靠任何一站。那么，在_____，客车能与3列货车先后相遇。
A: 在第四、五站之间
B: 在第五、六站之间
C: 在第六、七站之间
D: 在第七、八站之间
参考答案: B
本题解释:正确答案是B考点行程问题解析铁路上共有11个站，相邻两站相距7千米，则共有70千米的距离，每辆货车之间的距离是5千米。早晨8点，第一列货车已经开出60千米，与第一站相距10千米。客车和第一辆货车相遇时行驶路程为6.25千米，之后每行驶3.125公里即相遇一列货车，则相遇点距第一站点的距离是6.25+3.125n。要使客车在两个站点之间与连续3列货车相遇，则这三列货车中的第一列与客车相遇的地点距离站点不超过：7-3.125×2=0.75千米。即6.25+3.125n除以7余数<0.75，取n=7时商为4，余数为0.125<0.75。则客车行驶在第五、六站之间，分别和第8、9、10辆货车相遇。故正确答案为B。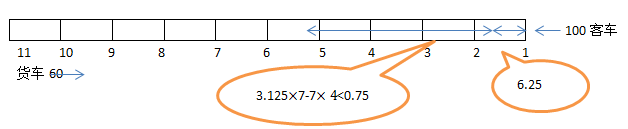

3、单选题  一艘游轮从甲港口顺水航行至乙港口需7小时，从乙港口逆水航行至甲港口需9小时。问如果在静水条件下，游轮从甲港口航行至乙港口需多少小时?_____
A: 7.75小时
B: 7.875小时
C: 8小时
D: 8.25小时
参考答案: B
本题解释:正确答案是B考点行程问题解析解析1：根据所需时间比，设距离为63，则游轮顺水和逆水的速度分别为9、7，则游轮自身的速度为(9+7)÷2=8，因此在静水条件下所需时间为63÷8=7.875小时。解析2：设甲乙港口相距距离为s，则游轮顺水和逆水的速度分别为s/7、s/9，游轮自身速度为(s/7+s/9)÷2，因此静水条件下所需时间为s÷[(s/7+s/9)÷2]=63÷8=7.875小时。标签顺水漂流模型赋值思想

4、单选题  自然数N是一个两位数，它是一个质数，而且N的个位数字与十位数字都是质数，这样的自然数有多少个?_____
A: 4
B: 6
C: 8
D: 12
参考答案: A
本题解释:正确答案是A考点排列组合问题解析由条件”N的个位数字与十位数字都是质数”可知，N只能是由2、3、5、7四个质数组合构成，可一一列举。此四个数字组合后构成如下质数：23、37、73、53。所以正确答案为A。标签数字特性

5、单选题  甲某打电话时忘记了对方电话号码最后一位数字，但记得这个数字不是"0"。甲某尝试用其他数字代替最后一位数字，恰好第二次尝试成功的概率是_____。
A: 1/9
B: 1/8
C: 1/7
D: 2/9
参考答案: A
本题解释:正确答案是A考点概率问题解析最后一个数字不是0，共有9种选择。要求恰好第二次尝试成功，则第一次尝试失败，概率为8/9，第二次更换数字成功，概率为1/8，因此恰好第二次尝试成功的概率为8/9×1/8=1/9。故正确答案为A。秒杀技根据不放回摸球模型，恰好第二次尝试成功的概率与恰好第一次成功的概率相同，因此该概率值为1/9。故正确答案为A。