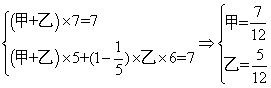1、单选题  一项工程，甲、乙两人合作4天后，再由乙单独做5天完成，已知甲比乙每天多完成这项工程的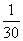A: 15，30
B: 10，15
C: 20，60
D: 12，20
参考答案: B
本题解释:参考答案:B
题目详解:已知：甲比乙每天多完成这项工程的

2、单选题  某工程甲单独做50天可以完成，乙单独做75天可以完成;现在两人合作，但途中乙因事离开了几天，最后一共花了40天把这项工程做完，则乙中途离开了_____天。
A: 15
B: 16
C: 22
D: 25
参考答案: D
本题解释:参考答案
题目详解:根据题意，设整个工程总量为“1”，则有：乙中途离开，但是甲从始至终工作了40天，那么甲的工作量为：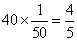

3、单选题  (2006江西)运送一批货物总运费为4200元，A、B两家运输公司同时运送8小时完成，A公司单独运输需14小时完成。现由A公司单独运送若干小时后，再由B公司单独运送剩下的货物。这样共用18小时全部运完。那么A、B两公司应分别获得：_____
A: 2100元，2100元
B: 600元，3600元
C: 1400元，2800元
D: 800元，3400元
参考答案: B
本题解释:参考答案:B
题目详解:解法一根据题意，设A、B两家运输公司的工作效率分别为x，y第一种运送方式的工作总量为：工作总量=工作效率×工作时间=8(x+y);第二种运送方式的工作总量为：工作总量=工作效率×工作时间=14x;由一二两种运送方式，得出8(x+y)=14x，解得x：y=4:3;第三种运送方式工作总量为：设现甲单独运送了t小时，则乙继续运送时间为(18-t)，工作总量=甲的工作总量+乙的工作总量=甲的工作效率×甲的工作时间+乙的工作效率×乙的工作时间=xt+y(18-t)，因为工作总量是一定的，所以xt+y(18-t)=14x，解得t=2;得出运输费用为:工作效率×工作时间×总费用，所以A运输公司所得费用：4200×1/14×2=600元;B公司的费用：4200-600=3600;因此，选B。解法二根据题意，设总工作量为"1”A公司的工作效率：工作效率=工作总量÷工作时间=1÷14=1/14;A、B公司的工作效率之和：工作效率=工作总量÷工作时间=1÷8=1/8;故B公司工作效率为:A、B公司工作效率之和-A工作效率=1/8-1/14=3/56;设A运送了t小时，则第三种运送方式的工作总量为：工作总量=工作效率×工作时间=1/14t+3/56(18-t)=1;解得t=2。得出运输费用为:工作效率×工作时间×总费用，所以A运输公司所得费用：4200×1/14×2=600元;B公司的费用：4200-600=3600;因此，选B。考查点:数量关系>数学运算>工程问题>合作完工问题

4、单选题  (2009吉林，第7题)甲、乙一起工作来完成一项工程，如果甲单独完成需要30天，乙单独完成需要24天，现在甲、乙一起合作来完成这项工程，但是乙中途被调走若干天，去做另一项任务，最后完成这项工程用了20天，问乙中途被调走_____天。
A: 8
B: 3
C: 10
D: 12
参考答案: D
本题解释:参考答案
题目详解:解法一：假设工程总量为“120”(30与24的最小公倍数)，由题意易知：甲的工作效率为：

5、单选题  (2009河北选调，第60题)甲、乙两队合作收割一块稻田，7小时可以完成。两队共同收割5小时后，甲队所有队员及乙队人数的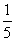A: 10
B: 12
C: 15
D: 20
参考答案: B
本题解释:参考答案:B
题目详解:解法一：假设工程总量为“7”，由题意易知：