1、单选题  有甲、乙、丙三辆公交车于上午8：00同时从公交总站出发，三辆车再次回到公交总站所用的时间分别为40分钟、25分钟和50分钟，假设这三辆公交车中途不休息，请问它们下次同时到达公交总站将会是几点?_____
A: 11点整
B: 11点20分
C: 11点40分
D: 12点整
参考答案: B
本题解释:正确答案是B考点周期问题解析三辆公交车下次同时到达公交总站相隔的时间应是三辆车周期的最小公倍数为200分钟，计3小时20分钟，因此三辆车下次同时到达公交总站的时间为11点20分钟。因此正确答案为B。标签最小公倍数

2、单选题  一个俱乐部，会下象棋的有69人，会下围棋的有58人，两种棋都不会下的有12人，两种棋都会下的有30人，问这个俱乐部一共有多少人?_____
A: 109人
B: 115人
C: 127人
D: 139人
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析由两集合容斥原理公式得俱乐部共有(69+58-30)+12=109人，故正确答案为A。两集合容斥原理公式：|A∪B|=|A|+|B|﹣|A∩B|。标签两集合容斥原理公式公式应用

3、单选题  小排量汽车每行驶100公里至少可节省1升汽油，假设一年行驶3万公里，每升汽油价格为4.26元，那么小排量汽车两年时间至少能节省的汽油费为_____。
A: 639元
B: 1278元
C: 2556元
D: 127800元
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析两年共行驶了6万公里，总共可以节省汽油60000/100=600升，所以节省的汽油费为600×4.26=6×426，利用尾数法可知，尾数为6，故正确答案为C。标签尾数法

4、单选题  一条双向铁路上有11个车站，相邻两站都相距7千米。从早晨7点，有18列货车由第11站顺次发出，每隔5分钟发一列，都驶向第一站，速度都是每小时60千米;早晨8点，由第1站发一列客车，向第11站驶出，时速100千米，在到达终点前，货车与客车都不停靠任何一站。那么，在_____，客车能与3列货车先后相遇。
A: 在第四、五站之间
B: 在第五、六站之间
C: 在第六、七站之间
D: 在第七、八站之间
参考答案: B
本题解释:正确答案是B考点行程问题解析铁路上共有11个站，相邻两站相距7千米，则共有70千米的距离，每辆货车之间的距离是5千米。早晨8点，第一列货车已经开出60千米，与第一站相距10千米。客车和第一辆货车相遇时行驶路程为6.25千米，之后每行驶3.125公里即相遇一列货车，则相遇点距第一站点的距离是6.25+3.125n。要使客车在两个站点之间与连续3列货车相遇，则这三列货车中的第一列与客车相遇的地点距离站点不超过：7-3.125×2=0.75千米。即6.25+3.125n除以7余数<0.75，取n=7时商为4，余数为0.125<0.75。则客车行驶在第五、六站之间，分别和第8、9、10辆货车相遇。故正确答案为B。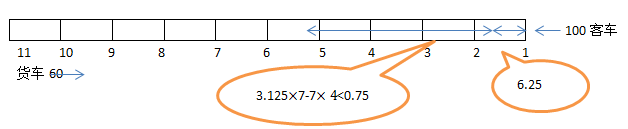

5、单选题  科学家对平海岛屿进行调查，他们先捕获30只麻雀进行标记，后放飞，再捕捉50只，其中有标记的有10只，则这一岛屿上的麻雀大约有_____。
A: 150只
B: 300只
C: 500只
D: 1500只
参考答案: A
本题解释:正确答案是A考点概率问题解析假设岛上有X只麻雀，捕捉30只进行标记，再捕捉50只，其中有10只有标记，则可列等式X∶30=50∶10，X=1500÷10=150(只)，故正确答案为A。