1、单选题  某一学校有500人，其中选修数学的有359人，选修文学的有408人，那么两种课程都选的学生至少有多少?_____。
A: 165人
B: 203人
C: 267人
D: 199人
参考答案: C
本题解释:C【解析】若一人只选修一门课程，则至少有359+408=767(人)，但该学校只有500人，多出的767-500=267(人)则是选两门课程的。故正确答案为C。

2、单选题  如图所示，圆O的面积为314平方米(π＝3.14)，平行四边形ABCD的面积为180平方米，则三角形ABO的面积是_____。
A: 49.5平方米
B: 48平方米
C: 47.5平方米
D: 45平方米
参考答案: D
本题解释:正确答案是D解析BO＝1/2BC，平行四边形面积＝BC×高＝180平方米，三角形面积＝BO×高×1/2＝BC×高×1/4＝1/4平行四边形面积＝45平方米，故正确答案为D。注：圆的面积是干扰项，不需要计算详细数据，只需比例转换。几何问题

3、单选题  A、B两地相距540千米。甲、乙两车往返行驶于A、B两地之间，都是到达一地之后立即返回，乙车较甲车快。设两辆车同时从A地出发后第一次和第二次相遇都在途中P地。那么两车第三次相遇为止，乙车共走了多少千米?（）
A: 120
B: 1440
C: 2160
D: 2880
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，可知：第一次相遇，甲、乙总共走了2个全程，第二次相遇，甲、乙总共走了4个全程，乙比甲快，相遇又在P点。所以可以推出：从第一次相遇到第二次相遇，甲从第一个P点到第二个P点，路程正好是第一次的路程，则P到A点的路程为P到B点路程的2倍。假设一个全程为3份，第一次相遇甲走了2份，乙走了4份;第二次相遇，乙正好走了1份到B地，又返回走了1份;2个全程里乙走了：(540÷3)×4=180×4=720千米，乙总共走了：720×3=2160千米。所以，选C考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题

4、单选题  下图是一个奥林匹克五环标志。这五个环相交成9部分：A、B、C、D、E、F、G、H、I。请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中，使得五环内的数字之和恰好构成五个连续的自然数。那么，这五个连续自然数的和的最大值是多少?_____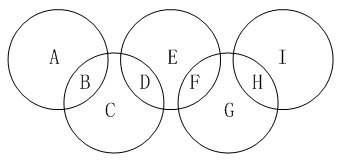A: 65
B: 75
C: 70
D: 102
参考答案: C
本题解释:正确答案是C考点趣味数学问题解析因为B、D、F、H同时出现在两个圆圈中而其他数都出现在一个圆圈中，所以五个圆圈中的总和为1+2+3+……+9+B+D+F+H≤45+9+8+7+6=75。若五个圆圈中的总和为75，则B+D+F+H=9+8+7+6=30，又因为五个环内的数字和恰好构成五个连续的自然数，所以这五个环内的数字只能是13、14、15、16、17，考虑两端两个圆圈中的总和，S=(A+B)+(H+I)≥13+14=27，但B+H≤9+8=17，A+I≤4+5=9，所以S最大为26，与上面的结论矛盾，所以五个圆圈中的总和不可能为75，又因为五个连续自然数的和是5的倍数，所以五个圆圈中的总和最大为70。当(A、B、C、D、E、F、G、H、I)=(9、7、3、4、2、6、1、8、5)时，五个圆圈的总和就可以取到70，故正确答案为C。

5、单选题  动物园的饲养员给三群猴子分花生，如只分给第一群，则每只猴子可得12粒;如只分给第二群，则每只猴子可得15粒;如只分给第三群，则每只猴子可得20粒，那么平均分给三群猴子.每只可得多少粒?_____
A: 3
B: 4
C: 5
D: 6
参考答案: C
本题解释:参考答案:C
题目详解:解法一：此题用特值法：设花生有60粒;那么第一群有