1、单选题  甲公司的一分厂制造了10台机床，二分厂制造了8台。乙公司向甲公司购买6台机床，丙公司向甲公司购买12台机床。每台机床的运费因运输距离的不同而有差异，具体情况如下表所示。乙、丙两公司购买机床的运费总和最低为_____元。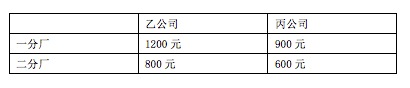A: 12000
B: 13500
C: 15000
D: 16000
参考答案: C
本题解释:正确答案是C考点统筹规划问题解析乙、丙公司从一分厂购买机床的价格分别为1200、900元，乙、丙公司从二分厂购买机床的价格分别为800、600元，乙、丙公司在一、二分厂的购买价格相差400、300元，为了使乙、丙两个公司的运费最低，二分厂的的机床都应该运至乙公司，乙丙最低运费为：6×800+2×600+(12-2)×900=4800+1200+9000=15000(乙公司买二分厂的6台机床，丙公司购买二分厂过剩余的2台机床和一分厂的10台机床)，故购买机床的最低运费为15000元。故正确答案为C。

2、单选题  若商品的进货价降低8%，而售价不变，那么利润(按进货价而定)可由目前的P%增加到(P+10)%。问P的值是_____。
A: 20
B: 15
C: 10
D: 5
参考答案: B
本题解释:正确答案是B考点经济利润问题解析解析1：设进货价为100元，因为利润为P%，所以售价为(100+P)元，因为进货价降低8%，即进货价为92元，此时利润为100+P-92=P+8，利润率为(P+8)/92=(P+10)%，解得P=15，故应选B。解析2：假定原进货价为a，由售价不变可列方程为：a×(1-8%)×[1+(P+10)%]=a×(1+P%)，解得P=15，故正确答案为B。

3、单选题  足球比赛的计分规则是：胜一场得3分，平一场得1分，负一场得0分，如果某国家足球队共打了28场比赛，其中负6场，共得40分，那么这个队胜了多少场?_____
A: 8
B: 10
C: 12
D: 9
参考答案: D
本题解释:正确答案是D考点鸡兔同笼问题解析解析1：这是鸡兔同笼问题的推广得得失问题，胜的场数和平的场数共有28-6=22(场)，根据得失问题公式，则胜的场数为(40-22)÷(3-1)=9(场)，故选D选项。注：比赛得失问题公式，﹙总的得分-平场数×平场得分)÷(胜场得分-平场得分)=胜的场数，(只有胜和平场时);(总的得分-平的场数×平场得分+输的场数×输场扣分)÷(胜场得分-平场得分+输场扣分)=胜的场数，(有胜、平、输场时)。解析2：胜的场数和平的场数共有28-6=22(场)，设胜的胜数为a，3×a+1×(22-a)=40，a=9(场)，故正确答案为D。标签公式应用

4、单选题  小王参加了五门百分制的测验，每门成绩都是整数，其中语文94分，数学的得分最高，外语的得分等于语文和物理的平均分，物理的得分等于五门的平均分，化学的得分比外语多2分，并且是五门中第二高的得分，问小王的物理考了多少分?_____
A: 94
B: 95
C: 96
D: 97
参考答案: C
本题解释:正确答案是C考点多位数问题解析已知语文94分，外语的得分等于语文和物理的平均分，而每门成绩都是整数，则可知物理成绩必为偶数，排除B、D;已知数学最高，化学第二高，物理为平均分，则物理不可能为94分，否则平均分大于94分，排除A。故正确答案为C。标签数字特性

5、单选题  某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8
B: 10
C: 12
D: 15
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人，可知乙培训过的人数含有因子3，而总的培训人数1290也含有因子3，因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人，因此要使甲教室培训过的人数也含有3因子，则其举办次数必然含有3因子，因此只有C、D符合。将C选项代入，可知此时乙教室举办过15次培训，其总人数的尾数为5，而甲教室培训的总人数尾数总是为0，因此甲、乙教室的培训人数尾数为5，不符合要求。故正确答案为D。秒杀技由题意，甲教室每次培训50人，乙教室每次培训45，假设甲乙的次数分别为X、Y，则可得50X+45Y=1290，观察等式可知45Y的尾数必然为0，因此Y必然为偶数，从而X为奇数，仅D符合。故正确答案为D。