1、单选题  一副扑克牌有52张，最上面一张是红桃A。如果每次把最上面的10张移到最下面而不改变它们的顺序及朝向，那么，至少经过多少次移动，红桃A会出现在最上面?_____
A: 27
B: 26
C: 25
D: 24
参考答案: B
本题解释:正确答案是B考点倍数约数问题解析每次移动扑克牌张数为10，因此移动的扑克牌总数必然是10的倍数;又红桃A从再最上面再回到最上面，则移动的扑克牌总数必然是52的倍数。10与52的最小公倍数是260，也即移动扑克牌数达到260后红桃A再次出现在最上面。移动次数为260÷10=26次，故正确答案为B。标签最小公倍数

2、单选题  甲、乙两人在长30米的泳池内游泳，甲每分钟游37.5米，乙每分钟游52.5米，两人同时分别从泳池的两端出发，触壁后原路返回，如是往返。如果不计转向的时间，则从出发开始计算的1分50秒内两人共相遇了多少次?_____
A: 2
B: 3
C: 4
D: 5
参考答案: B
本题解释:正确答案是B考点行程问题解析解析1：题目的关键在于第一次相遇，两人游过长度之和为泳池长，之后每次相遇，都需要两人再游过两个泳池长。两人一起游一个泳池长，所需时间为30÷(37.5+52.5)×60=20(秒)，因此两人分别在20秒时、60秒时、100秒时相遇，共相遇3次。故正确答案为B。解析2：关键点同解析1。直接求出1分50秒两人合起来游过的距离为(37.5+52.5)×110÷60=165(米)，为5.5个泳池长。而两人相遇时都恰是合起来游过距离为奇数个泳池长时，也即两人分别在合游1个、3个、5个泳池长时相遇，故共相遇3次。故正确答案为B。解析3：套用公式。先看迎面相遇，30×(2N-1)≤(37.5+52.5)×11/6，得N≤3.25，即有3次迎面相遇;再看追上相遇，30×(2N-1)≤(52.5-37.5)×11/6，得N≤23/24，即没有追及相遇。故总的相遇次数为3次。故正确答案为B。公式：两运动体从两端同时出发，相向而行，不断往返：第N次迎面相遇，两运动体路程和=全程×(2N-1);第N次追上相遇，两运动体路程差=全程×(2N-1)。标签公式应用

3、单选题  某俱乐部中女会员的人数比男会员的一半少61人，男会员的人数比女会员的3倍多2人，问该俱乐部共有会员多少人?_____
A: 475人
B: 478人
C: 480人
D: 482人
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析设女会员有X人，男会员为Y人，则有0.5Y-61=X，3X+2=Y，解得X=120，Y=362，总人数为120+362=482。故正确答案为D。秒杀技由题目第一个条件可知会员总数加上61后能被3整除，也即加上1后能被3整除，仅选项D符合。标签数字特性

4、单选题  某村村民经过集体投票民主选举村干部，5位村干部候选人中得票最高者将当选。经统计，本次选举有效选票一共395票，且当选者的得票数比其他4位候选人的平均得票数要多60票，则这名当选者一共获得_____票。
A: 62
B: 67
C: 122
D: 127
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析假定其他四位候选人的平均票数为M，则根据题意可得4M+M+60=395，解得M=67，因此当选者一共获得67+60=127票。故正确答案为D。

5、单选题  A: A
B: B
C: C
D: D
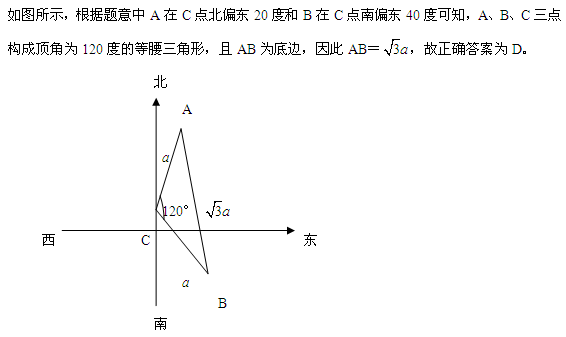
参考答案: D
本题解释:正确答案是D考点几何问题解析