1、单选题  x为正数，表示不超过x的质数的个数，如<5.1>=3，即不超过5.1的质数有2、3、5共3个。那么<<19>+<93>+<4>×<1>×<8>的值是：_____
A: 15
B: 12
C: 11
D: 10
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，分步计算：<19>为不超过19的质数，即2、3、5、7、11、13、17、19共8个。<93>为不超过93的质数，共24个，而<1>为不超过1的质数，为O个，那么<4>×<1>×<8>=0;则原式=<<19>+<93>>=<8+24>=<32>=11。所以，选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题

2、单选题  有一种数叫做完全数，它恰巧等于除去它本身以外的一切因数的和，如6是因数1+2+3的和。请问在20到30之间，这样的完全数是哪个?_____
A: 24
B: 26
C: 27
D: 28
参考答案: D
本题解释:参考答案
题目详解:根据题意，采用代入法对各项分析,只有28=1+2+4+7+14，其他选项都不符合题意。所以，选D。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题

3、单选题  如果5*2=5+6=11，6*3=6+7+8=21，那么1*9+2*9+3*9+…+9*9=_____。
A: 629
B: 729
C: 759
D: 829
参考答案: B
本题解释:参考答案:B
题目详解:根据题意，可知：5*2表示从5开始两个自然数相加;6*3表示从6开始的三个自然数相加;那么1*9=1+2+3+4+5+6+7+8+9，2*9=2+3+4+5+6+7+8+9+10，…9*9=9+10+11+12+13+14+15+16+17;分析，可知：1*9，2*9，…，9*9每组均有9个数字相加，且后面每一组里的9个数字均比前一组里的9个数字大1，即1*9，2*9，…，9*9构成公差为9，首项为1*9=1+2+…+9=45，项数为9的等差数列;故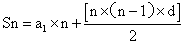

4、单选题  口、△、○分别代表三个数字，如果口÷△=○，则下列哪一个结论不正确?_____
A: 口=△×○
B: △=口×○
C: △=口÷○
D: 口=○×△
参考答案: B
本题解释:参考答案:B
题目详解:观察到B与C直接矛盾，必有一错，并且利用乘法规则，很容易看出B错。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题

5、单选题  已知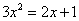B: 1
C: 2
D: 4
参考答案: C
本题解释:参考答案:C
题目详解:根据题干中