|
1、单选题 实验小学举办学生书法展,学校的橱窗里展出了每个年级学生的书法作品,其中有28幅不是五年级的,有24幅不是六年级的,五、六年级参展的书法作品共有20幅。一、二年级参展的作品总数比三、四年级参展的作品总数少4幅。一、二年级参展的书法作品共有多少幅?_____
A: 6
B: 10
C: 16
D: 20
参考答案: A
本题解释:参考答案:A
题目详解:28幅不是五年级的,也就是六年级+其他年级=28幅;24幅不是六年级的,也就是五年级+其他年级=24幅;上述两个式子相加得:(五年级+六年级)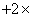 91EXAm.org 91EXAm.org g" ,因此,其他年级的=
2、单选题 如右图,三个图形共覆盖的面积为290,其中X、Y、Z的面积分别为64、180、160。X与Y、Y与Z、Z与X的重叠面积分别为24、70、36,求阴影部分面为_____。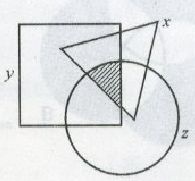 A: 12 A: 12
B: 16
C: 18
D: 20
参考答案: B
本题解释:参考答案:B
题目详解:由题意可知,假设阴影部分面积为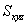
3、单选题 调查公司对甲、乙、丙三部电影的收看情况向125人进行调查,有89人看过甲片,47人看过乙片,63人看过丙片,24人三部都看过,20人一部也没有看过,问只有看过其中两部的有多少人?_____
A: 69
B: 65
C: 57
D: 46
参考答案: D
本题解释:参考答案
题目详解:考查文氏图运算。
4、单选题 五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩,其中语文成绩优秀的有65人,数学成绩优秀的有87人。语文、数学都优秀的有多少人?_____
A: 30
B: 35
C: 57
D: 65
参考答案: A
本题解释:参考答案:A
题目详解:此题是典型的两个集合的容斥问题,由题意设:A={{语文成绩优秀的人}};B={{数学成绩优秀的人}};因此,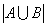
5、单选题 (2005国家一类,第45题)对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有多少人?_____
A: 22人
B: 28人
C: 30人
D: 36人
参考答案: A
本题解释:参考答案:A
题目详解:解法一:将题目条件代入下面三集合文氏图,凭借各部分加减关系依次标上相应数据: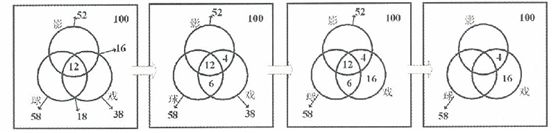
|