1、单选题  某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中都没有及格的有4人，那么两次考试都及格的人数是_____。
A: 22
B: 18
C: 28
D: 26
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析由题意，两次考试中至少有一次及格的人数为32-4=28(人)，设两次考试都及格的人数是n，则有：28=26﹢24-n，解得n=22。故正确答案为A。注：两集合容斥原理公式为A∪B=A+B-A∩B。标签两集合容斥原理公式

2、单选题  某农场有36台收割机，要收割完所有的麦子需要14天时间。现收割了7天后增加4台收割机，并通过技术改造使每台机器的效率提升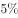A: 3
B: 4
C: 5
D: 6
参考答案: D
本题解释:正确答案是D，解析设每台收割机每天的工作效率为1，则工作总量为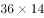

3、单选题  一个金鱼缸，现已注满水。有大、中、小三个假山，第一次把小假山沉入水中，第二次把小假山取出，把中假山沉入水中，第三次把中假山取出，把小假山和大假山一起沉入水中。现知道每次从金鱼缸中溢出水量的情况是：第一次是第二次的1/3，第三次是第二次的2倍。问三个假山的体积之比是多少?_____
A: 1：3：5
B: 1：4：9
C: 3：6：7
D: 6：7：8
参考答案: B
本题解释:正确答案是B考点和差倍比问题解析放入小假山，溢出水的体积为V，则小假山的体积为V;小假山取出，放入中假山，中假山除了将已溢出的体积V填满，还溢出3V体积的水，则中假山的体积是4V;同理，小假山和大假山除了将已溢出的体积4V填满，还溢出了6V，则大假山的体积为4V+6V-V=9V，可得三者之比为1：4：9。故正确答案为B。

4、单选题  从一副完整的扑克牌中至少抽出_____张牌，才能保证至少有5张牌的花色相同。
A: 17
B: 18
C: 19
D: 20
参考答案: C
本题解释:正确答案是C考点抽屉原理问题解析一副完整的扑克牌包括四种花色的A到K，共有4×13=52张以及2张大小王。要保证5张牌花色相同，根据抽屉原理，此时的"最不利"情形是每一种花色恰好不到5张，即红桃、方块、黑桃、梅花各抽出4张，且抽中了2张大小王，共计4×4﹢2=18张;最后抽出1张任意花色的牌，则可保证有5张花色相同。所以至少需要抽出18﹢1=19张牌，正确答案选C。

5、单选题  某市为合理用电，鼓励各用户安装峰谷电表，市原电价每度0.53元，改新表后，每晚10点至次日早8点为低谷，每度收0.28元，其余时间为高峰期，每度0.56元，为改装新电表每个用户须收取100元改装费，假定某用户每月用200度电，两个不同时段用电量各为100度，那么改装电表12个月后，该用户可节约_____元。
A: 161
B: 162
C: 163
D: 164
参考答案: D
本题解释:正确答案是D考点经济利润问题解析电表改装之前该用户每年的用电费用为200×0.53×12=1272元;改装电表之后，该用户这一年的用电费用加上改装费用共(0.28×100+0.56×100)×12+100=1108元，该用户改装电表前后可节约1272-1108=164元。故正确答案为D。