1、单选题  “红星”啤酒开展”7个空瓶换1瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期间共喝掉347瓶”红星”啤酒，问张先生最少用钱买了多少瓶啤酒?_____
A: 296瓶
B: 298瓶
C: 300瓶
D: 302瓶
参考答案: B
本题解释:正确答案是B考点计数模型问题解析7个空瓶换1瓶啤酒可表示为：7空瓶=1空瓶+1啤酒，可推知：6空瓶=1啤酒，假设最少要买x瓶，则有：x+[x/6]=347，将各选项代入知选项B中的298使得上述方程成立，故选择B选项。备注：此处的[x/6]表示取x/6的整数部分。标签直接代入

2、单选题  某通讯公司对3542个上网客户的上网方式进行调查，其中1258个客户使用手机上网，1852个客户使用有线网络上网，932个客户使用无线网络上网。如果使用不只一种上网方式的有352个客户，那么三种上网方式都使用的客户有多少个?_____
A: 148
B: 248
C: 350
D: 500
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析解析1：设三种上网方式都使用的客户有y个，则只使用两种方式上网的有(352-y)个，只使用一种方式上网的有(3542-352)个，根据题意可得：1258+1852+932=(3542-352)+2×(352-y)+3×y，解得y=148，因此三种上网方式都使用的客户有148个，故正确答案为A。解析2：设三种上网方式都使用的客户有y个，则只使用两种方式上网的有(352-y)个，前者重复计算了2次，后者重复计算了1次，根据题意可得：1258+1852+932-2y-(352-y)=3542，解得y=148，此三种上网方式都使用的客户有148个，故正确答案为A。备注：三集合容斥原理中，将只符合一个条件、只符合两个条件和三个条件都符合的分别看作三个整体，以A、B、C表示三个集合，以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分，则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z。标签三集合容斥原理公式整体考虑公式应用

3、单选题  一只木箱内有白色乒乓球和黄色乒乓球若干个。小明一次取出5个黄球、3个白球，这样操作N次后，白球拿完了，黄球还剩8个；如果换一种取法：每次取出7个黄球、3个白球，这样操作M次后，黄球拿完了，白球还剩24个。原木箱内共有乒乓球多少个？_____
A: 246个
B: 258个
C: 264个
D: 272个
参考答案: C
本题解释:正确答案是C解析乒乓球个数＝（3＋5）×N＋8＝8×（N＋1），即被8整除；乒乓球个数＝（7＋3）×M＋24＝10×（M＋2）＋4，即被10除余4；观察选项，只有C符合要求，故正确答案为C。

4、单选题  某学校的全体学生刚好排成一个方阵，最外层的人数是108人，则这个学校共有多少学生?_____
A: 724人
B: 744人
C: 764人
D: 784人
参考答案: D
本题解释:正确答案是D考点计数模型问题解析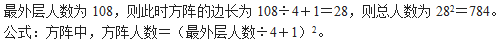

5、单选题  一张考试卷共有10道题，后面的每一道题的分值都比前面一道题多2分。如果这张考卷的满分为100分，那么第8道题的分值应为多少?_____
A: 14
B: 15
C: 16
D: 17
参考答案: B
本题解释:正确答案是B考点数列问题解析10道题的分值是公差为2的等差数列。设第一道题的分值为y，则第10道题的分值为y+2×(10-1)=y+18。由题意得(y+y+18)×10÷2=100，解得y=1，则第8道题的分值为1+2×(8-1)=15分，故正确答案为B。