1、单选题  (2003国家)姐弟俩出游，弟弟先走一步，每分钟走40米，走80米后姐姐去追他。姐姐每分钟走60米，姐姐带的小狗每分钟跑150米。小狗追上弟弟又转去找姐姐，碰上姐姐又转去追弟弟，这样跑来跑去，直到姐弟相遇小狗才停下来。问小狗共跑了多少米?_____
A: 600
B: 800
C: 1200
D: 1600
参考答案: A
本题解释:参考答案A
题目详解:由于小狗的运动规律不规则，但速度保持不变，故求出小狗跑的总时间即可。由于姐姐和小狗同时出发，同时终止。小狗跑的时间也就是姐姐追及弟弟的时间。设姐姐步行t分钟后和弟弟相遇，有：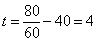

2、单选题  如右图所示，正方形ABCD的边长为5cm，AC、BD分别是以点D和点C为圆心、5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小_____。(π取3.14)
参考答案: B

3、单选题  现有篮球、排球、乒乓球、足球、网球五门选修课，每名学生必须要从中选出而且仅选择2门选修课，问至少有多少名学生进行选课，才能保证至少有6名学生所选的选修课相同？_____
A: 48
B: 50
C: 51
D: 70
参考答案: C
本题解释:【答案】C。解析：要求五门课程选出两门，共有C25=10种，要至少有6名学生所选的选修课相同，那么这10中选课方式各有5名学生选择，共有10×5=50人，之后再来一人，就可以保证有6名学生所选的选修课相同，则为50+1=51人，所以答案为C。

4、单选题  有20位运动员参加长跑，他们的参赛号码分别是1，2，3，……，20，至少要从中选出多少个参赛号码，才能保证至少有两个号码的差是13的倍数?_____
A: 12
B: 15
C: 14
D: 13
参考答案: C
本题解释:参考答案:C
题目详解:将这20个数字分别列为如下：(1，14)，(2，15)，(3，16)，…，(7，20)，8，9，10，11，12，13。考虑最差情况，就是前面抽出13个数字就是1-13，然后取第14个数字的时候不管取什么，肯定是14-20中的一个，与前面的数字相减必然能等于13。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1

5、单选题  一辆汽车驶过一座拱桥，拱桥的上下坡路程是一样的。汽车行驶拱桥上坡时的时速为6公里;下坡时的时速为12公里。则它经过该桥的平均速度是多少?_____
A: 7公里/小时
B: 8公里/小时
C: 9公里/小时
D: 10公里/小时
参考答案: B
本题解释:参考答案:B
题目详解:采用特殊数值法:可假设桥长24公里(此处假设的值需要方便计算);则上桥12公里用了2小时;下桥12公里用了1小时;则总共用了3小时：则速度为24÷3=8公里每小时。所以，选B。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值