1、单选题  某单位有60名运动员参加运动会开幕式，他们着装白色或黑色上衣，黑色或蓝色裤子。其中有12人穿白上衣蓝裤子，有34人穿黑裤子，29人穿黑上衣，那么穿黑上衣黑裤子的有多少人?_____
A: 12
B: 14
C: 15
D: 19
参考答案: C
本题解释:正确答案是C考点容斥原理问题解析解析1：穿白色上衣的有60-29=31人，其中穿白上衣黑裤子的有31-12=19人，穿黑上衣黑裤子的有34-19=15人。解析2：设白上衣黑裤子有a人，黑上衣黑子裤有b人，黑上衣蓝裤子有c人，根据题意有a+b+c=60-12，a+b=34，b+c=29，则b=34+29-(60-12)=15人。故正确答案为C。

2、单选题  一条双向铁路上有11个车站，相邻两站都相距7千米。从早晨7点，有18列货车由第11站顺次发出，每隔5分钟发一列，都驶向第一站，速度都是每小时60千米;早晨8点，由第1站发一列客车，向第11站驶出，时速100千米，在到达终点前，货车与客车都不停靠任何一站。那么，在_____，客车能与3列货车先后相遇。
A: 在第四、五站之间
B: 在第五、六站之间
C: 在第六、七站之间
D: 在第七、八站之间
参考答案: B
本题解释:正确答案是B考点行程问题解析铁路上共有11个站，相邻两站相距7千米，则共有70千米的距离，每辆货车之间的距离是5千米。早晨8点，第一列货车已经开出60千米，与第一站相距10千米。客车和第一辆货车相遇时行驶路程为6.25千米，之后每行驶3.125公里即相遇一列货车，则相遇点距第一站点的距离是6.25+3.125n。要使客车在两个站点之间与连续3列货车相遇，则这三列货车中的第一列与客车相遇的地点距离站点不超过：7-3.125×2=0.75千米。即6.25+3.125n除以7余数<0.75，取n=7时商为4，余数为0.125<0.75。则客车行驶在第五、六站之间，分别和第8、9、10辆货车相遇。故正确答案为B。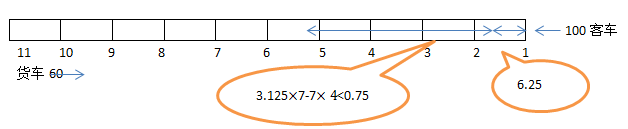

3、单选题  从一副完整的扑克牌中至少抽出_____张牌，才能保证至少有5张牌的花色相同。
A: 17
B: 18
C: 19
D: 20
参考答案: C
本题解释:正确答案是C考点抽屉原理问题解析一副完整的扑克牌包括四种花色的A到K，共有4×13=52张以及2张大小王。要保证5张牌花色相同，根据抽屉原理，此时的"最不利"情形是每一种花色恰好不到5张，即红桃、方块、黑桃、梅花各抽出4张，且抽中了2张大小王，共计4×4﹢2=18张;最后抽出1张任意花色的牌，则可保证有5张花色相同。所以至少需要抽出18﹢1=19张牌，正确答案选C。

4、单选题  某家具店购进100套桌椅，每套进价200元，按期望获利50%定价出售，卖掉60套桌椅后，店主为了提前收回资金，打折出售余下的桌椅，售完全部桌椅后，实际利润比期望利润低了18%，余下的桌椅是打_____出售的。
A: 七五折
B: 八二折
C: 八五折
D: 九五折
参考答案: C
本题解释:正确答案是C考点经济利润问题解析根据题意可得，期望利润为：200×50%×100=10000，则实际利润为：10000×(1-18%)=8200，设余下的折扣为y，原来售价为：200×(1+50%)=300，则有：300×60+300×y×(100-60)=200×100+8200，解得y=0.85，即八五折，故正确答案为C。

5、单选题  某公司100名员工对甲、乙两名经理进行满意度评议，对甲满意的人数占全体参加评议的3/5，对乙满意的人数比甲的人数多6人，对甲乙都不满意的占满意人数的1/3多2人，则对甲乙都满意的人数是_____。
A: 36
B: 26
C: 48
D: 42
参考答案: D
本题解释:正确答案是D考点容斥原理问题解析对甲满意的人数为60人，对乙满意的人数为66人，设对甲、乙都满意的人数为X，则对甲、乙都不满意的人数为1/3X+2，由两集合容斥原理的推论公式可知，100-(1/3X+2)=60+66-X，解得X=42，故正确答案为D。两集合容斥原理推论公式：满足条件1的个数+满足条件2的个数-都满足的个数=总数-都不满足的个数。