1、单选题  单独完成某项工作，甲需要16小时，乙需要12小时，如果按照甲、乙、甲、乙……的顺序轮流工作，每次1小时，那么完成这项工作需要多长时间?_____
A: 13小时40分钟
B: 13小时45分钟
C: 13小时50分钟
D: 14小时
参考答案: B
本题解释:正确答案是B考点工程问题解析设工作总量为48，则甲、乙的效率分别为3、4，因此甲乙工作一轮的工作量为7，因此甲乙可以先轮流6轮。完成6轮后，还剩工作量为6，此后甲又工作了一小时，完成工作量为3，还剩3，需要乙用45分钟。因此完成这项工作需要13小时45分钟，故正确答案为B。标签赋值思想

2、单选题  甲、乙两个港口相距120公里，船从甲到乙顺水航行需要5小时，从乙到甲逆水航行需要20小时。现有A、B两条船分别从甲、乙两港同时出发，相向而行，5小时后C船从甲港出发驶往乙港，则A、B相遇后_____小时，B、C相遇。
A: 6.5
B: 5.2
C: 4
D: 3
参考答案: C
本题解释:参考答案:.C
题目详解:船顺水航行速度为：

3、单选题  甲、乙合作完成一项工作，由于配合得好，甲的工作效率比单独做时提高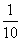A: 15
B: 16
C: 17
D: 18
参考答案: D
本题解释:参考答案
题目详解:根据题意，可知：甲、乙合作的效率是：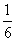

4、单选题  在前100个自然数中，能被3除尽的数相加，所得到的和是多少?_____
A: 1250
B: 1683
C: 1275
D: 1400
参考答案: B
本题解释:参考答案:B本题得分:
题目详解:根据题意，在前100中，能被3除尽的数，即个位数字之和为3的倍数;“在前100个自然数中，能被3整除的数”有3、6、9、12、15、18……故可以转化为首项为3，末项为99，公差为3，共有33项的等差数列;在前100个自然数中，能被3除尽的数的和——等差数列求和：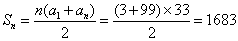

5、单选题  从某车站以加速度为 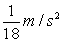A: 9
B: 3
C: 5
D: 6
参考答案: D
本题解释:参考答案D
题目详解:确定甲列车在行驶9分钟之后的终速度：对于匀变速而言，终速度=初始速度+加速度×时间，初始速度为0m/s，故甲列车在行驶9分钟之后的速度为：0+1/18×540=30m/s(注意单位统一);求距离最近的时间：设速度相等时乙列车运行时间为t秒，根据终速度=初始速度+加速度×时间，初始速度为0m/s，则50=0+1/18×(9×60+t)，解得t=360秒，即6分钟。所以，选D，考查点:数量关系>数学运算>行程问题>追及问题>直线追及问题>直线多次追及问题