1、单选题  某市为合理用电，鼓励各用户安装“峰谷”电表。该市原电价为每度0.53元，改装新电表后，每天晚上10点至次日早上8点为“低谷”，每度收取0.28元，其余时间为“高峰”，每度收取0.56元。为改装新电表每个用户须收取100元改装费。假定某用户每月用200度电，两个不同时段的耗电量各为100度。那么改装电表12个月后，该用户可节约_____元。
A: 161
B: 162
C: 163
D: 164
参考答案: D
本题解释:参考答案
题目详解:解法一：用户改装新表12个月共花费电费(0.28×100+0.56×100)×12=1008元，改装费100元，则：改装后所有花费为：1008+100=1108元;改装前所耗电费为：0.53×200×12=1272元;所以共节省：1272-1108=164元。解法二：根据题意，可知此题分为两个时间段。由于2个时间段都是100度，相当于每200度(一个周期)节约了：

2、单选题  某篮球比赛14:00开始，13:30允许观众入场，但早有人来排队等候入场，假设从第一个观众来到时起，每分钟来的观众人数一样多，如果开3个入场口，13:45时就不再有人排队，如果开4个入场口，13:40就没有人排队，那么第一个观众到达的时间是：_____
A: 13:00
B: 13:05
C: 13:10
D: 13:15
参考答案: A
本题解释:【答案】A。解析：设每个入场口每分钟可以进1人，则每分钟到达的观众为（3×15-4×10）÷（15-10）=1，到13:45时，总共有45人入场，需要45分钟，则第一个观众到达时间为13:00。

3、单选题  已知29832983…298302能被18整除，那么n的最小值是_____。
A: 4
B: 5
C: 6
D: 7
参考答案: A
本题解释:【解析】18=2×9，这个多位数的个位上是2，满足被2整除，因此，只需考虑个位数字之和能否被9整除的问题。（2+9+8+3）×n+0+2=22n+2是9的倍数，22×4+2=90=9×10，那么n的最小值为4。

4、单选题  已知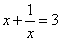A: 9
B: 8
C: D: 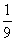参考答案: C
本题解释:参考答案:C
题目详解:原式的倒数为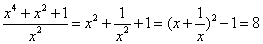

5、单选题  某商品2月份价格较1月份上涨了20%，由于政府调控政策的出台，3月份该商品价格又下降了20%，问该商品3月份的价格与1月份的价格相比_____。
A: 涨高了
B: 持平
C: 降低了
D: 不能确定
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析假定该商品1月份价格为100，则2月份价格为120，3月份价格为120×0.8=96，因此该商品3月份的价格比1月份有所降低，故正确答案为C。秒杀技降低时基数更大，因此降的更多，故3月份比1月份价格降低了，故正确答案为C。标签赋值思想