1、单选题  有20位运动员参加长跑，他们的参赛号码分别是1，2，3，……，20，至少要从中选出多少个参赛号码，才能保证至少有两个号码的差是13的倍数?_____
A: 12
B: 15
C: 14
D: 13
参考答案: C
本题解释:参考答案:C
题目详解:将这20个数字分别列为如下：(1，14)，(2，15)，(3，16)，…，(7，20)，8，9，10，11，12，13。考虑最差情况，就是前面抽出13个数字就是1-13，然后取第14个数字的时候不管取什么，肯定是14-20中的一个，与前面的数字相减必然能等于13。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1

2、单选题  实验小学举办学生书法展，学校的橱窗里展出了每个年级学生的书法作品，其中有28幅不是五年级的，有24幅不是六年级的，五、六年级参展的书法作品共有20幅。一、二年级参展的作品总数比三、四年级参展的作品总数少4幅。一、二年级参展的书法作品共有多少幅?_____
A: 6
B: 10
C: 16
D: 20
参考答案: A
本题解释:参考答案:A
题目详解:28幅不是五年级的，也就是六年级+其他年级=28幅;24幅不是六年级的，也就是五年级+其他年级=24幅;上述两个式子相加得：(五年级+六年级)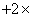

3、单选题  小明和小强从400米环形跑道的同一点出发，背向而行。当他们第一次相遇时，小明转身往回跑;再次相遇时，小强转身往回跑;以后的每次相遇分别是小明和小强两人交替调转方向。小明每秒跑3米，小强每秒跑5米，则在两人第30次相遇时。小明共跑了多少米? _____
A: 11250
B: 13550
C: 10050
D: 12220
参考答案: A
本题解释:A。两人相向运动，经过400÷（3+5）=50秒相遇，之后小明转身，两人做追及运动，经过400÷（5-2）=200秒第二次相遇;接着两人又做相向运动，经过50秒相遇，再做追及运动，经过200秒相遇，以此类推，第30次相遇共用30÷2×（50+200）=3750秒，则小明共跑了3×3750=11250米。

4、单选题  从某车站以加速度为 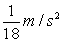A: 9
B: 3
C: 5
D: 6
参考答案: D
本题解释:参考答案D
题目详解:确定甲列车在行驶9分钟之后的终速度：对于匀变速而言，终速度=初始速度+加速度×时间，初始速度为0m/s，故甲列车在行驶9分钟之后的速度为：0+1/18×540=30m/s(注意单位统一);求距离最近的时间：设速度相等时乙列车运行时间为t秒，根据终速度=初始速度+加速度×时间，初始速度为0m/s，则50=0+1/18×(9×60+t)，解得t=360秒，即6分钟。所以，选D，考查点:数量关系>数学运算>行程问题>追及问题>直线追及问题>直线多次追及问题

5、单选题  女儿2013年时的年龄是母亲年龄的1/4，40年后女儿的年龄是母亲年龄的2/3。问当女儿年龄是母亲年龄的1/2时是公元多少年？_____
A: 2021       
B: 2022      
C: 2026       
D: 2029
参考答案: D
本题解释:【答案】D。