1、单选题  某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8
B: 10
C: 12
D: 15
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人，可知乙培训过的人数含有因子3，而总的培训人数1290也含有因子3，因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人，因此要使甲教室培训过的人数也含有3因子，则其举办次数必然含有3因子，因此只有C、D符合。将C选项代入，可知此时乙教室举办过15次培训，其总人数的尾数为5，而甲教室培训的总人数尾数总是为0，因此甲、乙教室的培训人数尾数为5，不符合要求。故正确答案为D。秒杀技由题意，甲教室每次培训50人，乙教室每次培训45，假设甲乙的次数分别为X、Y，则可得50X+45Y=1290，观察等式可知45Y的尾数必然为0，因此Y必然为偶数，从而X为奇数，仅D符合。故正确答案为D。

2、单选题  某次数学竞赛设一、二等奖。已知(1)甲、乙两校获奖的人数比为 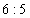A: 20
B: 30
C: 50
D: 60
参考答案: C
本题解释:参考答案:C
题目详解:已知甲、乙两校获二等奖的人数之比为5:6，那么设甲获二等奖的人数为5份，乙为6份。因为二等奖的人数占两校人数总和的60%，那么甲校获二等奖人数占总数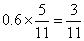

3、单选题  某高校2006年度毕业学生7650名，比上年度增长2%，其中本科生毕业数量比上年度减少2%，而研究生毕业数量比上年度增加10%，那么，这所高校今年毕业的本科生有_____。
A: 3920人
B: 4410人
C: 4900人
D: 5490人
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析假设去年研究生毕业数为A，本科生毕业数为B，那么今年研究生毕业数为1.1A，本科生毕业数为0.98B。由题意知：A+B=7650÷(1+2%)，1.1A+0.98B=7650，解得B=5000人。则今年本科生毕业数量为5000×0.98=4900人，故正确答案为C。秒杀技由“本科生比上年度减少2%”可知“今年本科生数=98%×去年本科生数”(注意98%是百分数，本质上也是个分数)，所以今年本科生应能够被49整除。由“研究生毕业数量比上年增加10%”知“今年研究生数=110%×去年研究生数”，所以今年研究生数应能够被11整除，据此两条得出正确答案为C。

4、单选题  某城市共有A、B、C、D、E五个区，A区人口是全市人口的5/17，B区人口是A区人口的2/5，C区人口是D区和E区人口总数的5/8，A区比C区多3万人，全市共有多少万人?_____
A: 20.4
B: 30.6
C: 34.5
D: 44.2
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析由A区人口是全市人口的5/17，将全市人口看做17份，则A区有5份，B区有2份，于是C、D、E三区共有10份，而在此三区中，C区人口是D区和E区人口总数的5/8，也即C区人口是此三区人口总数的5/13，因此C区人口为(5/13×10)份，于是A区比C区多5-50/13=15/13份，此部分人口数为3万人，于是全市共有3÷15/13×17=44.2(万人)。故正确答案为D。标签赋值思想

5、单选题  某汽车厂离生产甲、乙、丙三种车型，其中乙型产量的3倍与丙型产量的6倍之和等于甲型产量的4倍，甲型产量与乙型的2倍之和等于丙型产量的7倍。则甲、乙、丙三型产量之比为_____。
A: 5:4:3
B: 4:3:2
C: 4:2:1
D: 3:2:1
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析设甲的产量为x，乙的产量为y，丙的产量为z。则可得如下：3y+6z=4x，x+2y=7z，两式相加可得3x+z=5y，直接带入选项，只有D符合，故正确答案为D。秒杀技得到3y+6z=4x后，观察该式，可知x应为3的倍数，只有D符合。标签直接代入