1、单选题  (2006国考B类)某工作组有12名外国人，其中6人会说英语，5人会说法语，5人会说西班牙语;有3人既会说英语又会说法语，有2人既会说法语又会说西班牙语，有2人既会说西班牙语又会说英语;有1人这三种语言都会说。则只会说一种语言的人比一种语言都不会说的人多：_____
A: 1人
B: 2人
C: 3人
D: 5人
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，设：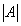

2、单选题  某单位围墙外面的公路围成了边长为300米的正方形，甲乙两人分别从两个对角沿逆时针同时出发，如果甲每分钟走90米，乙每分钟走70米，那么经过多少时间甲才能看到乙?_____
A: 16分40秒
B: 16分
C: 15分
D: 14分40秒
参考答案: A
本题解释:参考答案A
题目详解:如图所示:甲、乙的起始位置分别为甲0、乙0，甲要想看到乙，两人的距离最多300米。由甲、乙的追及问题可知：他们从开始相距600来到300米共需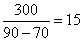

3、单选题  在春运高峰时，某客运中心售票大厅站满等待买票的旅客，为保证售票大厅的旅客安全，大厅入口处旅客排队以等速度进入大厅按次序等待买票，买好票的旅客及时离开大厅。按照这种安排，如果开10个售票窗口，5小时可使大厅内所有旅客买到票;如果开12个售票窗口，3小时可使大厅内所有旅客买到票，假设每个窗口售票速度相同。由于售票大厅入口处旅客速度增加到原速度的1.5倍，为了在2小时内使大厅中所有旅客买到票，按这样的安排至少应开售票窗口数为_____个。
A: 15
B: 16
C: 18
D: 19
参考答案: C
本题解释:C。设每个窗口的服务速度为x人/小时，大厅入口处旅客速度为y人/小时，大厅内乘客有s人。开10个售票窗口，5小时可使大厅内所有旅客买到票，说明s+5y=5×10x;开12个售票窗口，3小时可使大厅内所有旅客买到票，说明s+3y=3×12x;y=72，s=15x。大厅入口处旅客速度增加到原速度的1.5倍，即1.5y，要想在2小时内使大厅中所有旅客买到票，按这样的安排至少应开售票窗口数为t个，s+2×1.5y=2×tx，解得t=18。

4、单选题  三位采购员定期去某市场采购，小王每隔9天去一次，大刘每隔6天去一次，老杨每隔7天去一次，三人星期二第一次在这里，下次相会将在星期几?_____
A: 星期一
B: 星期五
C: 星期二
D: 星期四
参考答案: C
本题解释:正确答案是C考点倍数约数问题解析此题乍看上去是求9、6、7的最小公倍数的问题，但这里有一个关键词，即“每隔”，“每隔9天”也即“每10天”，所以此题实际上是求10、7、8的最小公倍数。10、7、8的最小公倍数是5×2×7×4=280。280÷7=40，所以下次相遇肯定还是星期二。秒杀技秒杀1：既然该公倍数是7的倍数，那么肯定下次相遇也是星期二。秒杀2：大刘每隔6天去一次，也即每七天去一次，因此大刘始终在星期二去，故下次相遇还会是星期二。标签最小公倍数数字特性

5、单选题  一群人坐车旅游，每辆车坐22人，剩5人没有座位，每辆坐26人，空出5个座位， 问每辆车坐25人，空出多少座位? _____
A: 20 
B: 15 
C: 10 
D: 5
参考答案: C
本题解释: C。一盈一亏型，车的数量为（15+5）÷ （26-22）=5,则共有5×22+5=115人。则坐25人时，115 ÷ 25=4……15，即需要5辆车，空出25-15=10个座位。