1、单选题  某班有50名学生，在第一次测验中有26人得满分，在第二次测验中有21人得满分。如果两次测验中都没有得满分的学生有17人，那么两次测验中都获得满分的人数是多少?_____
A: 13
B: 14
C: 17
D: 20
参考答案: B
本题解释:正确答案是B考点容斥原理问题解析本题注意按照得满分得到两个类，进行容斥原理分析。设第一次测验得满分为事件A，第二次测验得满分为事件B，则两次都得满分为A∩B，将其设为x人，得过满分为A∪B。根据公式A∪B=A+B-A∩B可得：50-17=26+21-x解得x=14，因此两次测验中都获得满分的人数是14人，故正确答案为B。标签两集合容斥原理公式

2、单选题  河流赛道长120米，水流速度2米/秒，甲船速度为6米/秒，乙船速度为4米/秒。比赛进行两次往返，甲、乙同时从起点出发，先顺水航行，问多少秒后甲、乙船第二次迎面相遇?_____
A: 48
B: 50
C: 52
D: 54
参考答案: C
本题解释:正确答案是C考点行程问题解析由于水速为2米/秒，所以顺行时候甲船速度是8米/秒，乙船速度是6米/秒。逆行时候甲船速度是4米/秒，乙船速度是2米/秒。甲乙的两次相遇分别在甲船第一次返回和甲船第二次顺行途中，甲第一次返回原地花费时间为120/8+120/4=45秒，此时乙到达对岸，逆水往回走，两船距离120-(4-2)×(45-120/6)=70米，再次相遇需要的时间为70÷(8+2)=7。所以总时间为45+7=52秒。故正确答案为C。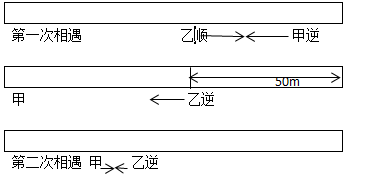

3、单选题  254个志愿者来自不同的单位，任意两个单位的志愿者人数之和不少于20人，且任意两个单位志愿者的人数不同，问这些志愿者所属的单位数最多有几个?_____
B: 1
C: 2
D: 3
参考答案: B
本题解释:正确答案是C考点趣味数学问题解析设A<B<C<D<E，则必有A+B=17，A+C=25，C+E=42，D+E=45。两两相加，应该有10个数值，因此必有两个重复值。这10个数值相加，必为4的倍数，将题中8个数值相加得261，除以4余1，因此另外两个加和必然除以4余3，重复的两个数在28、31、34、39中，因此这两个数为28、39或28、31，28必为重复值，可知B+C=A+D=28，所以，A=7，B=10，C=18，D=21，E=24，能被6整除的有18、24两个。故正确答案为C。<p>

4、单选题  某单位订阅了30份学习材料发放给3个部门，每个部门至少发放9份材料。问一共有多少种不同的发放方法?_____
A: 7
B: 9
C: 10
D: 12
参考答案: C
本题解释:正确答案是C考点排列组合问题解析

5、单选题  一只猎豹锁定了距离自己200米远的一只羚羊，以108千米/小时的速度发起进攻，2秒钟后，羚羊意识到危险，以72千米/小时的速度快速逃命。问猎豹捕捉到羚羊时，羚羊跑了多少路程?_____
A: 520米
B: 360米
C: 280米
D: 240米
参考答案: C
本题解释:正确答案是C考点行程问题解析猎豹的速度为108千米/小时，即30m/s，当羚羊意识到危险时，二者距离为200-30×2=140m，而羚羊的速度为72千米/小时，即20m/s;这是一个运动追及问题，故可得140÷(30-20)=14s，即羚羊从开始跑到被追上一共用了14s，共跑了20×14=280m。故正确答案为C。