1、单选题  计算：(1×2×3+2×4×6+…+100×200×300)/(2×3×4+4×6×8+…+200×300×400)的值为_____。
A: 1/8 
B: 1/4 
C: 3/2 
D: 5/4
参考答案: B
本题解释:B【解析】分析分子部分每个加数(连乘积)的因数，可以发现前后之间的倍数关系，从而把“1×2×3”作为公因数提到前面，分母部分也做类似的变形。原式=1×2×3+8×(1×2×3)+…+1000000×(1×2×3)2×3×4+8×(2×3×4)+…+1000000×(2×3×4)=[1×2×3×(1+8+…+1000000)]/[2×3×4×(1+8+…+1000000)]=(1×2×3)/(2×3×4)=1/4因此，本题正确答案为B。

2、单选题  已知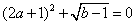A: B: C: D: 参考答案: B
本题解释:参考答案:B
题目详解:由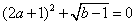

3、单选题  某人登山,上山时每走30分钟,休息10分钟;下山时每走30分钟,休息5分钟;下山的速度是上山速度的1.5倍。如果下山用了2小时15分,那么上山用的时间是_____。
A: 3小时40分 
B: 3小时50分
C: 4小时 
D: 4小时10分
参考答案: B
本题解释:【答案】B。解析:设上山速度是1,下山的速度是1.5,下山的时间是135分钟,那么走了4个30分钟,休息了3个5分钟,也就是走了2小时,那么路程就是1.5×2=3,上山时速度是1,时间就是3÷1=3小时,也就是走了6个30分钟,这需要休息5个10分钟,总共就用了3小时50分钟。

4、单选题  在1000以内，除以3余2，除以7余3，除以11余4的数有多少个?_____
A: 4
B: 5
C: 6
D: 7
参考答案: B
本题解释:正确答案是B考点余数与同余问题解析同余问题，不符合“余同取余，和同加和，差同减差，最小公倍数做周期”的口诀，通过余数组获得通式。除以3余2的余数组为2、5、8、11、14、17、···;除以7余3的余数组为3、10、17、···。结合此两者可知满足前两条的被除数可写成21n+17，其余数组为17、38、59、···;而除以11余4的余数组为4、15、26、37、48、59、···。结合此两者可知满足三条的被除数可写成231n+59。由题意：0≤231n+59≤1000，解得0≤n≤4。所以这样的数共有5个，故正确答案为B。口诀解释：余同取余，例如“一个数除以7余1，除以6余1，除以5余1”，可见所得余数恒为1，则取1，被除数的表达式为210n+1;和同加和，例如“一个数除以7余1，除以6余2，除以5余3”，可见除数与余数的和相同，取此和8，被除数的表达式为210n+8;差同减差，例如“一个数除以7余3，除以6余2，除以5余1”，可见除数与余数的差相同，取此差4，被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。

5、单选题  甲乙两个乡村阅览室，甲阅览室科技类书籍数量的1/5相当于乙阅览室该类书籍的1/4，甲阅览室文化类书籍数量的2/3相当于乙阅览室该类书籍的1/6，甲阅览室科技类和文化类书籍的总量比乙阅览室两类书籍的总量多1000本，甲阅览室科技类书籍和文化类书籍的比例为20:1，问甲阅览室有多少本科技类书籍?_____
A: 15000
B: 16000
C: 18000
D: 20000
参考答案: D
本题解释:答案：D.[解析]假设甲阅览室科技类书籍有20x本，文化类书籍有x本，则乙阅读室科技类书籍有16x本，文化类书籍有4x本，由题意有：（20x+x）-（16x+4x）=1000，解出x=1000，则甲阅览室有科技类书籍20000本。