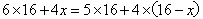1、单选题  有两根长短粗细不同的蚊香，短蚊香可燃8小时，长蚊香可燃的时间是短蚊香的1/2，同时点燃两根蚊香，经过3小时，它们的长短正好相等，未点燃之前，短蚊香比长蚊香短_____。
A: 1/6
B: 1/5
C: 1/2
D: 3/5
参考答案: D
本题解释:D【解析】两根蚊香同时点燃3小时后所剩长度相等，从这里我们可以找出长、短蚊香的长度关系：短蚊香点燃3小时后剩1-1× 3/8=5/8，长蚊香点燃3小时后剩1-（1×3）/（8×1/2）=1/4，即短蚊香的5/8等于长蚊香的1/4，由此可求出短蚊香是长蚊香的几分之几，即5/8短=1/4长，短/长=2/5，所以未点燃之前，短蚊香比长蚊香短1-2/5=3/5。

2、单选题  某单位向希望工程捐款，其中部门领导每人捐50元，普通员工每人捐20元，某部门所有人员共捐款320元。已知该部门部门总人数超过10人，问该部分可能有几名部门领导?_____
A: 1
B: 2
C: 3
D: 4
参考答案: B
本题解释:正确答案是B考点不定方程问题解析假定该部门领导、普通员工分别为X、Y，根据题意可得，50X+20Y=320，X+Y>10。改写上述方程为5X+2Y=32，可知X必为偶数，排除A、C;将其余选项代入验证，若X=2，则Y=11，X+Y=13>10，符合要求;若X=4，则Y=6，X+Y=10，不符合要求。故正确答案为B。

3、单选题  物美超市的收银台平均每小时有60名顾客前来排队付款，每一个收银台每小时能应付80名顾客付款。某天某时刻，超市如果只开设一个收银台，付款开始4小时就没有顾客排队了，问如果当时开设两个收银台，则付款开始几小时就没有顾客排队了?_____。
A: 2小时
B: 1.8小时
C: 1.6小时
D: 0.8小时
参考答案: D
本题解释:正确答案是D考点牛吃草问题解析假定超市原来排队的人数为N，每小时新增顾客人数为60人，只开1个收银台，4个小时后没有顾客排队，则N=(80×1-60)×4=80(人)。若开两个收银台，则a小时后就没顾客排队，80=(80×2-60)×a，a=0.8，故正确答案为D。

4、单选题  一名外国游客到北京旅游，他要么上午出去游玩，下午在旅馆休息，要么上午休息，下午出去游玩，而下雨天他只能一天都待在屋里。期间，不下雨的天数是12天，他上午待在旅馆的天数为8天，下午待在旅馆的天数为12天，他在北京共待了多少天?_____
A: 16天
B: 20天
C: 22天
D: 24天
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析解析1：设这个人在北京共待了n天，其中12天不下雨，那么n-12天下雨。由两集合容斥原理公式得：上午待在旅馆的天数+下午待在旅馆的天数-上下午都待在旅馆的天数(就是下雨的天数)=总天数-上下午都不待在旅馆的天数(根据题意不存在这样的一天)。即：8+12-(n-12)=n-0，解得n=16。故正确答案为A。解析2：设游客在京期间下雨天数为x。因为他上午待在旅馆的8天中包括两部分：因下雨无法出去的天数(x)和因下午出去游玩而休息的天数(8-x);同理，下午待在旅馆的12天中包括两个部分：因下雨无法出去的天数(x)和因上午出去游玩而休息的天数(12-x)。由题意可得：(8-x)+(12-x)=12，解得x=4，所以一共在北京待了16天。故正确答案为A。

5、单选题  甲、乙、丙三个工程队的效率比为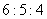A: 6
B: 7
C: 8
D: 9
参考答案: A
本题解释:参考答案:A
题目详解:解法一：由题意可设甲、乙、丙每日工作量分别为6、5、4，丙队参与A工程x天，那么参加B工程(16-x)天，根据A、B工作量相同可列方程：