1、单选题  学校五(一)班40名学生中，年龄最大的是13岁，最小的是11岁，那么其中至少有多少名学生是同年同月出生的?_____
B: 1
C: 2
D: 3
参考答案: C
本题解释:参考答案:C
题目详解:解法一：把同年同月的放在一组里面，那么每一组可以作为1个“抽屉”;因此，可以构成3×12=36个“抽屉”，40÷36=1…4;由抽屉原理1可以得到，至少有2名学生是同年同月出生的。解法二：这40名同学的年龄最多相差36个月(三年)，因40=1×36+4,故必有2人是同年、同月出生的。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1

2、单选题  一把钥匙只能开一把锁，现在有10把锁和其中的8把钥匙，请问至多需要试验多少次，才能够保证一定将这8把钥匙都配上锁?_____
A: 52
B: 44
C: 18
D: 8
参考答案: B
本题解释:参考答案:B
题目详解:第1把钥匙最多试9次，能够将这把钥匙配上锁;第2把钥匙最多试8次，能够将这把钥匙配上锁;……;第8把钥匙最多试2次，能够将这把钥匙配上锁。因此，最多需要试验9+8+…+2=44次，才能够保证一定将8把钥匙都配上锁。所以，选B。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1

3、单选题  某商店有126箱苹果，每箱至少有120个苹果，至多有144个苹果。现将苹果个数相同的箱子算作一类。设其中箱子数最多的一类有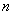A: 4
B: 5
C: 6
D: 7
参考答案: C
本题解释:参考答案:C
题目详解:解法一：将苹果个数相同的箱子算成一类，那么每一类都可以看成一个“抽屉”。这样可以构造出144-120+1=25个抽屉，又由于：126÷25=5…1，由抽屉原理2可以得到，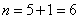

4、单选题  有关部门要连续审核30个科研课题方案，如果要求每天安排审核的课题个数互不相等且不为零，则审核完这些课题最多需要_____。
A: 7天
B: 8天
C: 9天
D: 10天
参考答案: A
本题解释:参考答案:A
题目详解:每天审核的课题应尽可能少，才能增加审核天数。假设第1天审核1个，则第2天最少审核2个，……依此类推,则审核完这些课题天数最多的方案应为每天审核1，2，3，4，5，6，9或1，2，3，4，5，7，8。显然所需天数都为7天。所以，选A。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1

5、单选题  有20位运动员参加长跑，他们的参赛号码分别是1，2，3，……，20，至少要从中选出多少个参赛号码，才能保证至少有两个号码的差是13的倍数?_____
A: 12
B: 15
C: 14
D: 13
参考答案: C
本题解释:参考答案:C
题目详解:将这20个数字分别列为如下：(1，14)，(2，15)，(3，16)，…，(7，20)，8，9，10，11，12，13。考虑最差情况，就是前面抽出13个数字就是1-13，然后取第14个数字的时候不管取什么，肯定是14-20中的一个，与前面的数字相减必然能等于13。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1