1、单选题  汽车往返甲、乙两地之间，上行速度为30公里/时，下行速度为60公里/时，汽车往返的平均速度为_____公里/时。
A: 40
B: 45
C: 50
D: 55
参考答案: A
本题解释:正确答案是A考点工程问题解析解析1：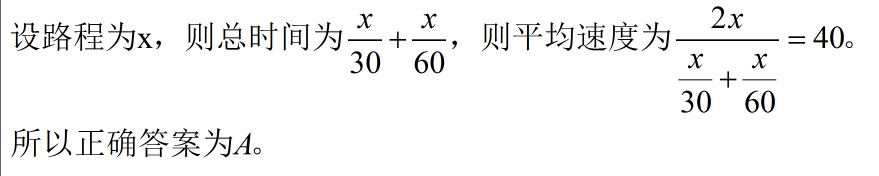

2、单选题  6个空瓶可以换一瓶汽水，某班同学喝了157瓶汽水，其中有一些是用喝剩下来的空瓶换的，那么他们至少要买多少瓶汽水?_____
A: 131
B: 130
C: 128
D: 127
参考答案: A
本题解释:正确答案是A考点计数模型问题解析典型的空瓶换水问题，根据等价公式，6个空瓶可换一瓶水→6空瓶=1瓶水+1空瓶→5空瓶=1瓶水。设买了x瓶汽水，有x+x/5=157，解得x=130.8，取整得x=131，即至少要买131瓶水，故正确答案为A。等价公式：若M个空瓶换一瓶水，相当于M-1个空瓶可以喝到1瓶水。

3、单选题  某工程项目由甲项目公司单独做，需4天完成，由乙项目公司单独做，需6天才能完成，甲、乙、丙三个公司共同做2天就可以完成，现因交工日期在即，需多公司合作，但甲公司因故退出，则由乙、丙公司合作完成此项目共需多少天?_____
A: 3
B: 4
C: 5
D: 6
参考答案: B
本题解释:正确答案是B考点工程问题解析由题意可设总工程量为12(4、6、2的公倍数)，所以甲的效率为12/4=3，乙的效率为12/6=2，丙的效率为12/2-3-2=1，所以若乙丙合作需要12÷(2+1)=4天。故正确答案为B。

4、单选题  箱子中有编号1—10的10个小球，每次从中抽出一个记下编号后放回，如果重复3次，则3次记下的小球编号乘积是5的倍数的概率是多少?_____
A: 43.2%
B: 48.8%
C: 51.2%
D: 56.8%
参考答案: B
本题解释:正确答案是B考点概率问题解析若3次记下的小球编号乘积是5的倍数，则至少有一次需要抽到5或10。其反面是一次5或10都没有抽到，这种情况的概率为0.8×0.8×0.8=0.512。故3次记下的小球编号乘积是5的倍数的概率为1-51.2%=48.8%。故正确答案为B。

5、单选题  有46名学生需要到河对岸去参观明清时期的古民居。现只有一条船，每条船最多载6人(其中1人划船)，往返一次需要7分钟，如果早晨8点钟准时开始渡河，到8点38分时，至少还有多少人在等待渡河?_____
A: 10
B: 15
C: 20
D: 25
参考答案: B
本题解释:正确答案是B考点计数模型问题解析由题意，38÷7=5......3，故到8点38分时，共往返5次，此时已经开始第6次过河，前5次渡河后需要1人划船返回，因此共有5×(6-1)+6=31人已经过河或者正在过河，在河边等待的还有46-31=15人，故正确答案为B。