1、单选题  甲乙两人相约见面，并约定第一人到达后，等15分钟不见第二人来就可以离去。假设他们都在10点至10点半的任一时间来到见面地点，则两人能见面的概率有多大?_____
A: 37.5%
B: 50%
C: 62.5%
D: 75%
参考答案: D
本题解释:正确答案是D考点概率问题解析本题为几何概率问题。设甲到达的时间为10点x分，乙到达的时间为10点y分，则只有|x-y|≤15，甲乙才能相遇。本题可以采用作图法求解，甲、乙到达约定地点的情况(0≤x≤30，0≤y≤30)如下图，则只有在阴影部分区域甲乙能够相遇，也就是求阴影部分的面积的比例。由图中可以看出，阴影部分占总面积的3/4，即两人能见面的概率为75%。故正确答案为D。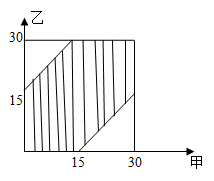

2、单选题  中午12点，甲驾驶汽车从A地到B地办事，行驶1小时，走了总路程的15%。此后甲的速度增加了15公里/小时，又行驶了30分钟，距离B地还有3/4的路程。此后甲的速度如果再增加15公里/小时，问几点能到B地?_____
A: 16：00
B: 16：30
C: 17：00
D: 17：30
参考答案: B
本题解释:正确答案是B，全站数据:本题共被作答1次，正确率为0.00%，易错项为D解析假设原来甲的速度为x，第1小时行驶总路程15%，随后的30分钟行驶10%，则根据行程问题的方程列出比例关系xx+15)=15:10可以解得x=45。所以之前的1小时30分钟一共行驶了45+30=75，剩余路程为75×3=225。所以需要时间225÷75=3，故需要4.5小时，最终16:30到达。故正确答案为B。考点行程问题笔记编辑笔记

3、单选题  一个游泳池，甲管注满水需6小时，甲、乙两管同时注水，注满要4小时。如果只用乙管注水，那么注满水需_____小时。
A: 14
B: 12
C: 10
D: 8
参考答案: B
本题解释:正确答案是B考点工程问题解析解析1：该题为工程问题，直接赋值求解，甲单独完成注水，时间为6小时，甲和乙共同注水时间是4小时，取最小公倍数为12作为总工程量。则甲和乙一起注水4小时，甲完成的工作量12×4/6=8，乙完成的工作量为12-8=4份，乙每小时完成1份工作量，单独注水需要12个小时完成12份工作量。故正确答案为B。解析2：该问题为工程问题，可以比例转化求解。赋值工程量为6，甲单独注水时间为6，甲乙同注水4小时，甲完成的工程量是6×4/6=4，则乙完成的工程量是6-4=2，则甲乙效率比为2:1，单独注水时间比为1:2。则乙单独注水需要12小时。标签比例转化

4、单选题  某成衣厂对9名缝纫工进行技术评比，9名工人的得分一给好成等差数列，9人的平均得分是86分，前5名工人的得分之和是460分，那么前7名工人的得分之和是多少?_____
A: 602
B: 623
C: 627
D: 631
参考答案: B
本题解释:正确答案是B考点平均数问题解析由于前5名工人的得分之和是460分，则第三名工人的得分=460÷5=92(分)，9人的平均得分是86分，即第五名工人的得分为86分，所以第四名的得分为(92+86)÷2=89(分)，所以前7名的总分为89×7=623(分)，故正确答案为B。注释：等差数列的平均数等于其中位数的值。

5、单选题  3×999+8×99+4×9+15的值是_____。
A: 3866
B: 3855
C: 3840
D: 3877
参考答案: C
本题解释:正确答案是C考点计算问题解析计算原式个位上的数字，7+2+6+5=20，个位数为0，故正确答案为C。