1、单选题  一个水库在年降水量不变的情况下，能够维持全市12万人20年的用水量，在该市新迁入3万人之后，该水库只够维持15年的用水量，市政府号召节约用水，希望能将水库的使用寿命提高到30年。那么，该市市民平均需要节约多少比例的水才能实现政府制定的目标?_____
A: 2/5
B: 2/7
C: 1/3
D: 1/4
参考答案: A
本题解释:正确答案是A考点牛吃草问题解析假设原有水量为X，单位时间进水量Y，根据题意可得：X=(12-Y)×20，X=(15-Y)×15，解得X=180，Y=3。假设用30年可供N万人次，则可得，180=(N-3)×30，解得N=9。也即15万人的用水量相当于9万人，因此节水比例为2/5，故正确答案为A。

2、单选题  有水果糖、奶糖、巧克力三袋重量不同的糖果，水果糖与奶糖的重量比是6：5，若水果糖的2/3被吃掉，且被吃掉的水果糖与被吃掉的巧克力的重量之比是5：4，那么这两种糖剩下的部分重量相等。问原先水果糖、奶糖、巧克力的重量之比是多少？_____
A: 35：30：31
B: 25：20：21
C: 30：25：26
D: 42：35：40
参考答案: C
本题解释:C。

3、单选题  建华中学共有1600名学生，其中喜欢乒乓球的有1180人，喜欢羽毛球的有1360人，喜欢篮球的有1250人，喜欢足球的有1040人，问以上四项球类运动都喜欢的至少有几人?_____
A: 20人
B: 30人
C: 40人
D: 50人
参考答案: B
本题解释:正确答案是B考点抽屉原理问题解析采取逆向思维法。不喜欢乒乓的1600-1180=420，不喜欢羽毛球的1600-1360=240，不喜欢篮球的1600-1250=350，不喜欢足球的1600-1040=560，要使四项运动都喜欢的人数最少，那么不喜欢的人数就要最多那么都尽量不相交，从而达到最多：420+240+350+560=1570人，所以喜欢的最少的为1600-1570=30人，故正确答案为B。

4、单选题  把自然数按由小到大的顺序排列起来组成第一串数：1、2、3、……、9、10、11、12、……把这串数中两位以上的数全部隔开成一位数字，组成第二串数：1、2、……、9、1、0、1、1、1、2、1、3、……。则第一串数中100的个位数字0在第二串数中是第几个数?_____
A: 188
B: 198
C: 192
D: 202
参考答案: C
本题解释:正确答案是C考点多位数问题解析根据题意，第一串数一位数(1—9)有9个，可分成9个数字;两位数(10—99)有99-10+1=90个，可分成90×2=180个数，则第一串数中100的个位数0在第二串数字中的位置为9+180+3=192，故正确答案为C。

5、单选题  连接正方体每个面的中心构成一个正八面体(如下图所示)。己知正方体的边长为6厘米，问正八面体的体积为多少立方厘米?_____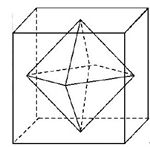A: 182
B: 242
C: 36
D: 72
参考答案: C
本题解释:正确答案是C考点几何问题解析正八面体可以拆解成两个完全相同的四棱锥，每个棱锥的体积V=1/3Sh，高度h为正方体边长的一半，h=3厘米，棱锥的底面是下面正方体横截面(从正中切开)里的小正方形，因此棱锥的底面积是正方体底面积的一半：6×6÷2=18平方厘米，每个棱锥的体积为1/3×18×3=18立方厘米，该正八面体的体积为18×2=36立方厘米，故正确答案为C。