1、单选题  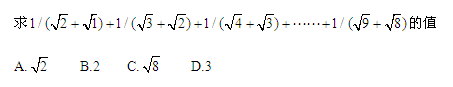_____ A: A
B: B
C: C
D: D
参考答案: B
本题解释:正确答案是B考点计算问题解析

2、单选题  某人月初用一笔人民币投资股票，由于行情较好，他的资金每月都增加1/3。即使他每月末都取出1000元用于日常开销，他的资金仍然在3个月后增长了一倍。问他开始时投资了多少人民币?_____
A: 9900元
B: 9000元
C: 12000元
D: 11100元
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析

3、单选题  用10张同样长的纸条粘接成一条长61厘米的纸条，如果每个接头处都重叠1厘米，那么每张纸条长_____厘米。
A: 7
B: 6.9
C: 6.1
D: 7.1
参考答案: A
本题解释:正确答案是A考点趣味数学问题解析设每张纸条长a厘米，每个接头重叠1厘米，则10张纸条共有9个接头，即9厘米，列出方程为10a-9=61，解得方程为a=7厘米，故正确答案为A。

4、单选题  林子里的猴子喜欢吃的野果，23只猴子可以在9周内吃光，21只猴子可以在12周内吃光，问如果有33只猴子一起吃，则需要几周吃光(假定野果生长的速度不变)?_____
A: 2周
B: 3周
C: 4周
D: 5周
参考答案: C
本题解释:正确答案是C考点牛吃草问题解析设原有野果为N，每周生长的野果可供Y个猴子吃，根据题意可得：N=(23-Y)×9，N=(21-Y)×12，解得N=72，Y=15。因此若33只猴子一起吃，需要时间为72÷(33-15)=4周。故正确答案为C。公式：在牛吃草模型背景下，公式为N=(牛数-Y)×天数，其中N表示原有草量的存量，以牛数与天数的乘积来衡量;Y表示专门吃新增加草量所需要的牛数。标签公式应用

5、单选题  用0、1、2、3、…、9十个数字组成5个两位数，每个数字只用一次，要求它们的和是一个奇数，并且尽可能大，问这五个两位数的和是多少?_____
A: 279
B: 301
C: 351
D: 357
参考答案: C
本题解释:正确答案是C考点多位数问题解析题目中涉及两个构造条件，一是和为奇数，二是和尽可能大，从后一个条件入手，应把10个数字中最大的5个放在十位上，即十位上的数字为5、6、7、8、9，个位上的数字为4、3、2、1、0，即可构造出和最大的5个两位数为54、63、72、81、90，但此时这5个数的和为偶数，需进一步调整。只需将个位上的某个奇数(或偶数)与十位上的某个偶数(或奇数)调换位置即可，同时又要保证和最大，因此选择个位和十位上的数字相差最小的54，调换位置后为45，此时5个数的和为45+63+72+81+90，根据尾数法可直接确定，故正确答案为C。标签构造调整尾数法