1、单选题  在1000以内，除以3余2，除以7余3，除以11余4的数有多少个?_____
A: 4
B: 5
C: 6
D: 7
参考答案: B
本题解释:正确答案是B考点余数与同余问题解析同余问题，不符合“余同取余，和同加和，差同减差，最小公倍数做周期”的口诀，通过余数组获得通式。除以3余2的余数组为2、5、8、11、14、17、···;除以7余3的余数组为3、10、17、···。结合此两者可知满足前两条的被除数可写成21n+17，其余数组为17、38、59、···;而除以11余4的余数组为4、15、26、37、48、59、···。结合此两者可知满足三条的被除数可写成231n+59。由题意：0≤231n+59≤1000，解得0≤n≤4。所以这样的数共有5个，故正确答案为B。口诀解释：余同取余，例如“一个数除以7余1，除以6余1，除以5余1”，可见所得余数恒为1，则取1，被除数的表达式为210n+1;和同加和，例如“一个数除以7余1，除以6余2，除以5余3”，可见除数与余数的和相同，取此和8，被除数的表达式为210n+8;差同减差，例如“一个数除以7余3，除以6余2，除以5余1”，可见除数与余数的差相同，取此差4，被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。

2、单选题  整数64具有可被它的个位数字所整除的性质。试问在10和50之间有_____个整数具有这种性质。_____
A: 15
B: 16
C: 17
D: 18
参考答案: C
本题解释:正确答案是C考点倍数约数问题解析个位是1、2、5的数字都可以被1、2、5整除，有4×3=12个;个位是3的数字十位必须是3的倍数才能被3整除，只有33这1个数字;个位是4的数字十位必须是偶数才能被4整除，有2个;个位是6的数字十位也必须是3的倍数，有1个;个位是7的数字十位必须能够被7整除，有0个;个位是8的数字十位必须是4的倍数，有1个。个位是9的十位必须是9的倍数，有0个。因此总共有12+1+2+1+0+1+0=17个。故正确答案为C。

3、单选题  一项工程计划用20天完成，实际只用了16天就完成了，则工作效率提高的百分率是_____。
A: 20%
B: 25%
C: 50%
D: 60%
参考答案: B
本题解释:正确答案是B考点工程问题解析工作时间比为16：20=4：5，效率与时间成反比，即5：4=125%，提高了25%，故正确答案为B。

4、单选题  _____ A: 1/6
B: 5/66
C: 7/85
D: 1/128
参考答案: B
本题解释:正确答案是B考点计算问题解析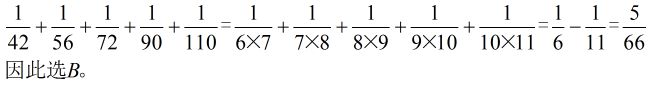

5、单选题  一个浴缸放满水需要30分钟，排光一浴缸水需要50分钟，假如忘记关上出水口，将这个浴缸放满水需要多少分钟?_____
A: 65分钟
B: 75分钟
C: 85分钟
D: 95分钟
参考答案: B
本题解释:正确答案是B考点牛吃草问题解析水缸的容量记为单位"1"，那么每分钟可以注入的水占水缸容量的1/30，每分钟排出的水占水缸容量的1/50。根据题意，水龙头在注入水的同时，部分水也在排出，所以实际上每分钟注入的水应该为1/30-1/50=1/75，则需要75分钟才能注满，故正确答案为B。