1、单选题  有1角、2角、5角和1元的纸币各1张，现在从中抽取至少1张，问可以组成不同的几种币值?_____
A: 18种
B: 17种
C: 16种
D: 15种
参考答案: D
本题解释:正确答案是D考点排列组合问题解析

2、单选题  有一笔奖金，按1：2：3的比例来分，已知第三人分450元，那么这笔奖金总共是_____元。
A: 1150
B: 1000
C: 900
D: 750
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析根据题意可知，三个奖金赋值份数为1，2，3份，这笔奖金共分为6份，而分到3份的第三人拿到了450元，则6份为450×2=900元。故正确答案为C。

3、单选题  某城市9月平均气温为28.5度，如当月最热日和最冷日的平均气温相差不超过10度，则该月平均气温在30度及以上的日子最多有多少天?_____
A: 24
B: 25
C: 26
D: 27
参考答案: B
本题解释:正确答案是B考点多位数问题解析要使30度以上的天数尽可能多，在气温总和一定的情况下，则必然是其他天的温度尽可能低，而由最热日与最冷日的平均气温相差不超过10度，据此构造极端情况，最热天全部为30度，其余天为最冷天，温度为20度，设平均气温为30度的天数为x，则可得30x+20(30-x)=30×28.5，解得x=25.5，因此最多有25天。故正确答案为B。

4、单选题  某城市居民用水价格为：每户每月不超过5吨的部分按4元/吨收取，超过5吨不超过10吨的部分按6元/吨收取，超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元，则该户居民这两个月用水总量最多为多少吨?_____
A: 21
B: 24
C: 17.25
D: 21.33
参考答案: A
本题解释:正确答案是A考点分段计算问题解析在花费相同的情况下，要使两个月用水量最多，须使水价相对较便宜阶段的用水量最大，即两个月的“不超过5吨”和“5吨到10吨”部分的水量尽量多，通过计算2×(4×5+6×5)=100元，剩余180-100=8元，由于超出10吨的部分按8元/吨收取，故用水量为2×10+1=21吨。故正确答案为A。

5、单选题  对厦门大学计算机系100名学生进行调查，结果发现他们喜欢看NBA和足球、赛车。其中58人喜欢看NBA;38人喜欢看赛车，52人喜欢看足球，既喜欢看NBA又喜欢看赛车的有18人，既喜欢看足球又喜欢看赛车的有16人，三种都喜欢看的有12人，则只喜欢看足球的有_____。
A: 22人
B: 28人
C: 30人
D: 36人
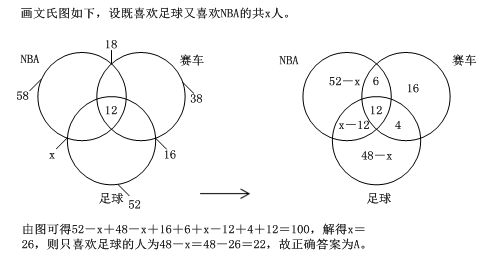
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析