1、单选题  从甲、乙两车站同时相对开出第一辆公共汽车，此后两站每隔8分钟再开出一辆，以此类推。已知每辆车的车速相同且都是匀速的，每辆车到达对方站都需要45分钟。现有一乘客坐甲站开出的第一辆车去乙站，问他在路上会遇到几辆从乙站开出的公共汽车。_____。
A: 4辆
B: 5辆
C: 6辆
D: 7辆
参考答案: C
本题解释:正确答案是C考点计数模型问题解析乘客从甲站出发，45分钟内共有6个时间段乙站会发车，出发时间分别为0、8、16、24、32、40分钟，故乘客在路会遇到6辆车，正确答案为C。

2、单选题  地上放着一个每一面上都有一个数的六面体箱子，对面两个数的和均为27，甲能看到顶面和两个侧面，这三个面上的数字之和是35;乙能看到顶面和另外两个侧面，且这三个面上的数字和为47。箱子贴地一面的数字是_____。
A: 14
B: 13
C: 12
D: 11
参考答案: B
本题解释:正确答案是B考点趣味数学问题解析题目给出对面数字之和为27，则注意将其余条件中出现的对面合在一起。从这一点出发，可以看出若将甲与乙看到的面合在一起，则实际共看到2个顶面与4个不同的侧面。而四个不同侧面恰为两组对面，也即其数字之和为27×2=54，因此顶面的数字为(35+47-54)÷2=14，于是底面数字为27-14=13，故正确答案为B。

3、单选题  为了浇灌一个半径为10米的花坛，园艺师要在花坛里布置若干个旋转喷头，但库房里只有浇灌半径为5米的喷头，问花坛里至少要布置几个这样的喷头才能保证每个角落都能浇灌到?_____
A: 4
B: 7
C: 6
D: 9
参考答案: B
本题解释:正确答案是B考点几何问题解析注意到对一个圆而言，圆弧是最外层，因此在浇灌时首先要保证整个圆弧能够被覆盖到。一个小圆只能覆盖一段圆弧，由于每个小圆的直径为10，也即一个小圆覆盖圆弧对应的弦最长为10，而大圆的半径为10，所以每个小圆至多盖住圆心角为60°所对应的弧长。因此想盖住整个圆圈，至少需要六个小圆，并且当且仅当这六个小圆以大圆的内接正六边形各边中点为圆心进行覆盖。此时大圆的圆心处尚未被覆盖，还需要一个小圆才能完成覆盖。如图所示，故正确答案为B。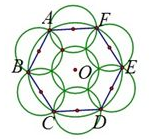

4、单选题  某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8
B: 10
C: 12
D: 15
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人，可知乙培训过的人数含有因子3，而总的培训人数1290也含有因子3，因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人，因此要使甲教室培训过的人数也含有3因子，则其举办次数必然含有3因子，因此只有C、D符合。将C选项代入，可知此时乙教室举办过15次培训，其总人数的尾数为5，而甲教室培训的总人数尾数总是为0，因此甲、乙教室的培训人数尾数为5，不符合要求。故正确答案为D。秒杀技由题意，甲教室每次培训50人，乙教室每次培训45，假设甲乙的次数分别为X、Y，则可得50X+45Y=1290，观察等式可知45Y的尾数必然为0，因此Y必然为偶数，从而X为奇数，仅D符合。故正确答案为D。

5、单选题  在一周长为50m的圆形花坛周围种树，如果每隔5m种一颗，共要种_____棵树。
A: 9
B: 10
C: 11
D: 12
参考答案: B
本题解释:正确答案是B考点计数模型问题解析根据圆周植树计算模型，始端与终端重合，故一共需种50÷5=10棵树，正确答案为B。标签公式应用