1、单选题  甲、乙、丙三人沿着200米的环形跑道跑步，甲跑完一圈要1分30秒，乙跑完一圈要1分20秒，丙跑完一圈要1分12秒，三人同时、同向、同地起跑，最少经过多少时间又在同一起跑线上相遇?_____
A: 10分
B: 6分
C: 24分
D: 12分
参考答案: D
本题解释:参考答案
题目详解:三人跑完一圈的时间比为：

2、单选题  (2008.辽宁)张警官一年内参与破获的各类案件有100多件，是王警官的5倍，李警官的五分之三，赵警官的八分之七，问李警官一年内参与破获多少案件?_____
A: 175
B: 105
C: 120
D: 不好估算
参考答案: A
本题解释:参考答案:A
题目详解:设张警官破获的案件为x件，则：根据“是王警官的5倍，李警官的五分之三，赵警官的八分之七”可知，张警官破获了5×3×7×N件，又因100故张警官破获的案件只能为105;则李警官一年内参与破获了案件：105÷3/5=175件。因此，选A。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>三个数的最大公约数和最小公倍数

3、单选题  在1到200的全部自然数中，既不是5的倍数，也不是8的倍数的数有多少个?_____
A: 25
B: 40
C: 60
D: 140
参考答案: D
本题解释:参考答案
题目详解:由题意得，5和8的最小公倍数是40。从1到200中，5的倍数有：200÷5=40个，8的倍数有：200÷8=25个，5和8的公倍数有：200÷40=5个，至少是5或者8的倍数的有：40+25-5=60个。所以，既不是5的倍数，也不是8的倍数的数有：200-60=140个。所以，选D。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数

4、单选题  园林工人要在周长300米的圆形花坛边等距离地栽上树，他们先沿着花坛的边每隔3米挖一个坑，当挖完30个坑时，突然接到通知：改为每隔5米栽一棵树。这样，他们还要挖多少个坑才能完成任务?_____。
A: 60
B: 54
C: 50
D: 56
参考答案: B
本题解释:参考答案:B
题目详解:根据题意，每隔3米已挖30个坑，所以实际挖了：3×30=90米;在90米内3、5的最小公倍数即15，则90米内求3、5的公倍数有：15、30、45、75、90，这五个数即为重复的坑;300米每隔5米栽一棵要所需要的坑的数量为：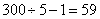

5、单选题  6.有两个两位数，这两个两位数的最大公约数与最小公倍数的和是91，最小公倍数是最大公约数的12倍，求这较大的数是多少?_____
A: 42
B: 38
C: 36
D: 28
参考答案: D
本题解释:参考答案
题目详解:此题可以根据定义来解答。这两个数的最大公约数是：