1、单选题  某民航飞机飞行在6个民航站之间，那么共有多少种机票?_____
A: 21种
B: 22种
C: 28种
D: 30种
参考答案: D
本题解释:正确答案是D考点排列组合问题解析从一个民航站起飞，有5种飞机票;现有6个民航站，则有5×6=30种机票。故正确答案为D。

2、单选题  一项工程，甲一人做完需30天，甲、乙合作完成需18天，乙、丙合作完成需15天，甲、乙、丙三人共同完成该工程需_____。
A: 10天
B: 12天
C: 8天
D: 9天
参考答案: A
本题解释:正确答案是A考点工程问题解析赋值总工程量为90，则甲效率为3，甲乙合作效率为5，故乙的效率为2;而乙丙合作效率为6，故丙的效率为4。于是甲乙丙效率之和为9，故三人合作该工程需要10天。因此答案选A。

3、单选题  41个学生要坐船过河，渡口处只有一只能载4人的小船(无船工)，他们要全部渡过河去，至少要使用这只小船渡河多少次_____
A: 23 
B: 24 
C: 27 
D: 26
参考答案: C
本题解释:【答案】C。解析：4个人渡过去，1个人回来，因此每2次渡河可以渡过去3个学生.41=3×13+2，因此一共需要13×2+1=27次。

4、单选题  19991998的末位数字是：_____
A: 1       
B: 3       
C: 7       
D: 9
参考答案: A
本题解释:【解析】此题关键是要考察末位数的变化情况，9的一次幂、二次幂、三次幂、四次幂……的尾数呈9、1、9、1……变化，即其奇数次幂时尾数是9，偶数次幂时尾数是1，所以，选A

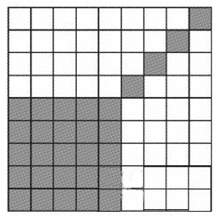
5、单选题  在9×9的方格表中，每行每列都有小方格被染成黑色，且一共只有29个小方格为黑色。如果a表示至少包含5个黑色小方格的行的数目，b表示至少包含5个黑色小方格的列的数目，则a+b的最大值是_____。
A: 25
B: 10
C: 6
D: 14
参考答案: B
本题解释:B【解析】假设a+b≥11，且a≥b，则2a≥11，因为不存在染半格的情况，所以a≥6。那么这a行中至少有黑色小方格6×5=30（个），与题干中只有29个黑色小方格的条件相矛盾，因此假设不成立，a+b≤10，当a+b=10时，黑色小方格的分布如下图。故本题答案为B。